Surface of revolution - AbsoluteAstronomy.com

A surface of revolution is a surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

in Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

created by rotating a curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

(the generatrix) around a straight line in its plane (the axis).

Examples of surfaces generated by a straight line are cylindrical

Cylinder (geometry)

A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...

and conical surface

Conical surface

In geometry, a conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex...

s when the line is coplanar with the axis, as well as hyperboloids of one sheet when the line is skew

Skew lines

In solid geometry, skew lines are two lines that do not intersect and are not parallel. Equivalently, they are lines that are not coplanar. A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron...

to the axis. A circle that is rotated about a diameter generates a sphere and if the circle is rotated about a coplanar axis other than the diameter it generates a torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

Area formula

If the curve is described by the parametric

Parametric

Parametric may refer to:*Parametric equation*Parametric statistics*Parametric derivative*Parametric plot*Parametric model*Parametric oscillator *Parametric contract*Parametric insurance*Parametric feature based modeler...

functions

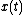, with

ranging over some interval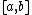

, and the axis of revolution is the

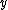-axis, then the area

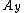is given by the integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

provided that

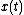is never negative. This formula is the calculus equivalent of Pappus's centroid theorem

Pappus's centroid theorem

In mathematics, Pappus' centroid theorem is either of two related theorems dealing with the surface areas and volumes of surfaces and solids of revolution....

. The quantity

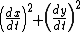
comes from the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

and represents a small segment of the arc of the curve, as in the arc length

Arc length

Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...

formula. The quantity

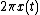is the path of (the centroid of) this small segment, as required by Pappus' theorem.

LIkewise, when the axis of rotation is the

-axis and provided that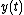

is never negative, the area is given by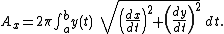

If the curve is described by the function y = f(x), a ≤ x ≤ b, then the integral becomes

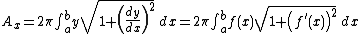
for revolution around the x-axis, and

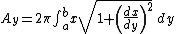
for revolution around the y-axis (Using a ≤ y ≤ b). These come from the above formula.

For example, the spherical surface

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

with unit radius is generated by the curve x(t) = sin(t), y(t) = cos(t), when t ranges over

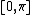. Its area is therefore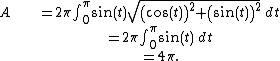

For the case of the spherical curve with radius

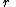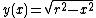rotated about the x-axis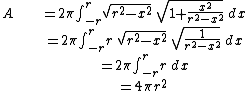

Rotating a function

To generate a surface of revolution out of any 2-dimensional scalar function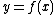

, simply make

the function's parameter, set the axis of rotation's function to simply

, then use

to rotate the function around the axis by setting the other two functions equal to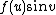

and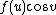

. For example, to rotate a function

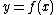around the x-axis starting from the top of the

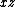-plane, parameterize it as

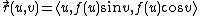for

and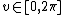

Geodesics on a surface of revolution

Geodesics on a surface of revolution are governed by Clairaut's relation.

Applications of surfaces of revolution

The use of surfaces of revolution is essential in many fields in physics and engineering. When certain objects are designed digitally, revolutions like these can be used to determine surface area without the use of measuring the length and radius of the object being designed.

External links

"Surface de révolution" at Encyclopédie des Formes Mathématiques Remarquables

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Area formula

Rotating a function

Geodesics on a surface of revolution

Applications of surfaces of revolution

See also

External links