
Liouville surface
Encyclopedia
In the mathematical
field of differential geometry a Liouville surface is a type of surface
which in local coordinates
may be written as a graph
in R3
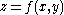
such that the first fundamental form
is of the form

Sometimes a metric
of this form is called a Liouville metric. Every surface of revolution
is a Liouville surface.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of differential geometry a Liouville surface is a type of surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
which in local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
may be written as a graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
in R3
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
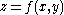
such that the first fundamental form
First fundamental form
In differential geometry, the first fundamental form is the inner product on the tangent space of a surface in three-dimensional Euclidean space which is induced canonically from the dot product of R3. It permits the calculation of curvature and metric properties of a surface such as length and...
is of the form

Sometimes a metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
of this form is called a Liouville metric. Every surface of revolution
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
is a Liouville surface.

