A channel or canal surface is a surface

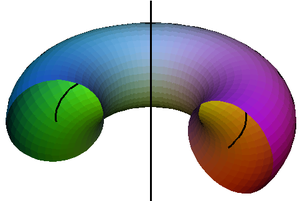
Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

 formed as the envelope

Envelope (mathematics)

In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...

 of a family of sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

s whose centers lie on a space curve. One sheet of the focal surface

Focal surface

For a surface in three dimension the focal surface, surface of centers or evolute is formed by taking the centers of the curvature spheres, which are the tangential spheres whose radii are the reciprocals of one of the principal curvatures at the point of tangency...

 of a channel surface will be the generating curve.

If the sphere centers lie on a straight line, the channel surface is a surface of revolution

Surface of revolution

A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....

. Dupin cyclides form a special class of surfaces which are channel surfaces in two distinct ways: for cyclides both sheets of the focal surface

Focal surface

For a surface in three dimension the focal surface, surface of centers or evolute is formed by taking the centers of the curvature spheres, which are the tangential spheres whose radii are the reciprocals of one of the principal curvatures at the point of tangency...

 are curves; in fact they are both conic section

Conic section

In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...

s.