
Limaçon
Encyclopedia
In geometry
, a limaçon or limacon (icon), also known as a limaçon of Pascal, is defined as a roulette
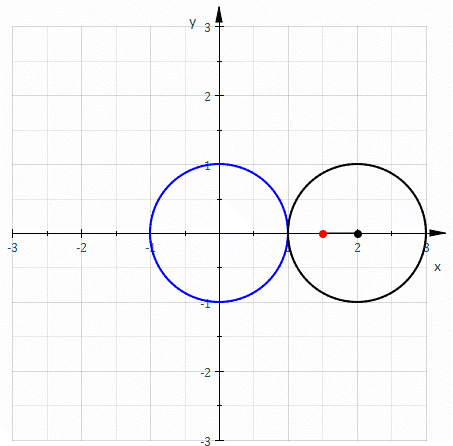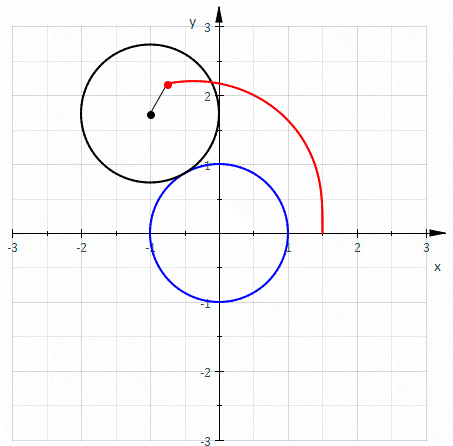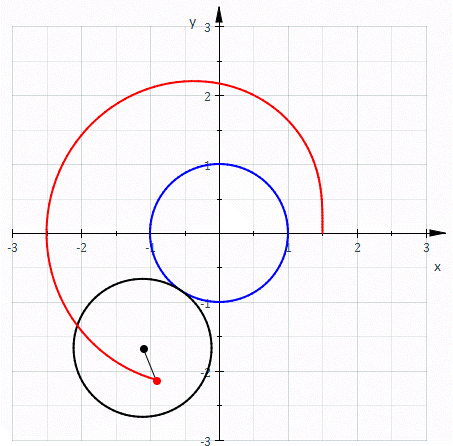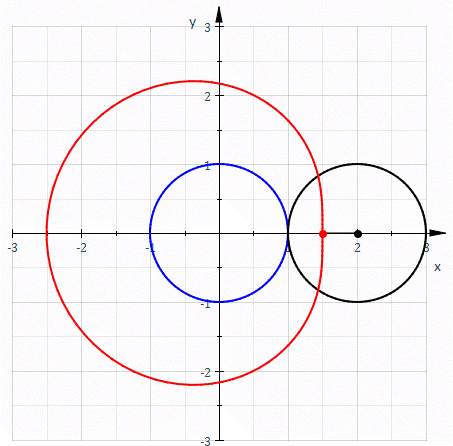
formed when a circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoid
s; more specifically, they are epitrochoid
s. The cardioid
is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp
.
The term derives from the Latin word limax, which means "snail
". Depending on the position of the point generating the curve, it may have inner and outer loops (giving the family its name), it may be heart
-shaped, or it may be oval.
A limaçon is a bicircular
rational plane algebraic curve
of degree
2.

, father of Blaise Pascal
. However, some insightful investigations regarding them had been undertaken earlier by the German
Renaissance
artist Albrecht Dürer
. Dürer's Underweysung der Messung (Instruction in Measurement) contains specific geometric methods for producing limaçons.

This can be converted to Cartesian coordinates by multiplying by r (thus introducing a point at the origin which in some cases is spurious), and substituting and
and  to obtain
to obtain

Parametrically, this becomes

In the complex plane
this takes the form

 If we shift this horizontally by a/2 we obtain the equation in the usual form for a centered trochoid:
If we shift this horizontally by a/2 we obtain the equation in the usual form for a centered trochoid:
This is the equation obtained when the center of the curve (as a centered trochoid) is taken to be the origin.
 or
or  making it a member of Sinusoidal spiral
making it a member of Sinusoidal spiral
family of curves. This curve is the Cardioid
In the special case the centered trochoid form of the equation becomes
the centered trochoid form of the equation becomes ,
,
or, in polar coordinates,

making it a member of the rose
family of curves. This curve is a trisectrix
, and is sometimes called the limaçon trisectrix
.
 the limaçon is a simple closed curve. However, the origin satisfies the Cartesian equation given above so the graph of this equation has an acnode
the limaçon is a simple closed curve. However, the origin satisfies the Cartesian equation given above so the graph of this equation has an acnode
or isolated point.
When the area bounded by the curve is convex and when
the area bounded by the curve is convex and when  the curve has an indentation bounded by two inflection point
the curve has an indentation bounded by two inflection point
s. At the point
the point  is a point of 0 curvature
is a point of 0 curvature
.
As is decreased relative to
is decreased relative to  , the indentation becomes more pronounced until, at
, the indentation becomes more pronounced until, at  , the cardioid, it becomes a cusp. For
, the cardioid, it becomes a cusp. For  , the cusp expands to an inner loop and the curve crosses itself at the origin. As
, the cusp expands to an inner loop and the curve crosses itself at the origin. As  approaches 0 the loop fills up the outer curve and, in the limit, the limaçon becomes a circle traversed twice.
approaches 0 the loop fills up the outer curve and, in the limit, the limaçon becomes a circle traversed twice.
 . When
. When  this counts the area enclosed by the inner loop twice. In this case the curve crosses the origin at angles
this counts the area enclosed by the inner loop twice. In this case the curve crosses the origin at angles  , the area enclosed by the inner loop is
, the area enclosed by the inner loop is
 , the area enclosed by the outer loop is
, the area enclosed by the outer loop is  , and the area between the loops is
, and the area between the loops is 
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a limaçon or limacon (icon), also known as a limaçon of Pascal, is defined as a roulette
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, and involutes....
formed when a circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoid
Centered trochoid
In geometry, a centered trochoid is the roulette formed by a circle rolling along another circle. That is, the path traced by a point attached to a circle as the circle rolls without slipping along a fixed circle. The term encompasses both epitrochoid and hypotrochoid...
s; more specifically, they are epitrochoid
Epitrochoid
An epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
s. The cardioid
Cardioid
A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp...
is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
.
The term derives from the Latin word limax, which means "snail
Snail
Snail is a common name applied to most of the members of the molluscan class Gastropoda that have coiled shells in the adult stage. When the word is used in its most general sense, it includes sea snails, land snails and freshwater snails. The word snail without any qualifier is however more often...
". Depending on the position of the point generating the curve, it may have inner and outer loops (giving the family its name), it may be heart
Heart
The heart is a myogenic muscular organ found in all animals with a circulatory system , that is responsible for pumping blood throughout the blood vessels by repeated, rhythmic contractions...
-shaped, or it may be oval.
A limaçon is a bicircular
Circular algebraic curve
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation F = 0, where F is a polynomial with real coefficients and the highest-order terms of F form a polynomial divisible by x2 + y2...
rational plane algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of degree
Degree of a continuous mapping
In topology, the degree is a numerical invariant that describes a continuous mapping between two compact oriented manifolds of the same dimension. Intuitively, the degree represents the number of times that the domain manifold wraps around the range manifold under the mapping...
2.

History
The earliest formal research on limaçons is generally attributed to Étienne PascalÉtienne Pascal
Étienne Pascal was the father of Blaise Pascal. His father and mother were Martin Pascal, the treasurer of France, and Marguerite Pascal de Mons. He also had three daughters, two of whom survived past childhood: Gilberte and Jacqueline...
, father of Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
. However, some insightful investigations regarding them had been undertaken earlier by the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
artist Albrecht Dürer
Albrecht Dürer
Albrecht Dürer was a German painter, printmaker, engraver, mathematician, and theorist from Nuremberg. His prints established his reputation across Europe when he was still in his twenties, and he has been conventionally regarded as the greatest artist of the Northern Renaissance ever since...
. Dürer's Underweysung der Messung (Instruction in Measurement) contains specific geometric methods for producing limaçons.
Equations
The equation (up to translation and rotation) of a limaçon in polar coordinates has the form
This can be converted to Cartesian coordinates by multiplying by r (thus introducing a point at the origin which in some cases is spurious), and substituting
 and
and  to obtain
to obtain
Parametrically, this becomes

In the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
this takes the form



This is the equation obtained when the center of the curve (as a centered trochoid) is taken to be the origin.
Special cases
In the special case a = b, the polar equation is or
or  making it a member of Sinusoidal spiral
making it a member of Sinusoidal spiralSinusoidal spiral
In geometry, the sinusoidal spirals are a family of curves defined by the equation in polar coordinatesr^n = a^n \cos\,where a is a nonzero constant and n is a rational number other than 0...
family of curves. This curve is the Cardioid
Cardioid
A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp...
In the special case
 the centered trochoid form of the equation becomes
the centered trochoid form of the equation becomes ,
,or, in polar coordinates,

making it a member of the rose
Rose (mathematics)
In mathematics, a rose or rhodonea curve is a sinusoid plotted in polar coordinates. Up to similarity, thesecurves can all be expressed by a polar equation of the form\!\,r=\cos.If k is an integer, the curve will be rose shaped with...
family of curves. This curve is a trisectrix
Trisectrix
In geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of...
, and is sometimes called the limaçon trisectrix
Limaçon trisectrix
In geometry, a limaçon trisectrix is a member of the Limaçon family of curves which has the trisectrix, or angle trisection, property...
.
Form
When the limaçon is a simple closed curve. However, the origin satisfies the Cartesian equation given above so the graph of this equation has an acnode
the limaçon is a simple closed curve. However, the origin satisfies the Cartesian equation given above so the graph of this equation has an acnodeAcnode
An acnode is an isolated point not on a curve, but whose coordinates satisfy the equation of the curve. The term "isolated point" or "hermit point" is an equivalent term....
or isolated point.
When
 the area bounded by the curve is convex and when
the area bounded by the curve is convex and when  the curve has an indentation bounded by two inflection point
the curve has an indentation bounded by two inflection pointInflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
s. At
 the point
the point  is a point of 0 curvature
is a point of 0 curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
.
As
 is decreased relative to
is decreased relative to  , the indentation becomes more pronounced until, at
, the indentation becomes more pronounced until, at  , the cardioid, it becomes a cusp. For
, the cardioid, it becomes a cusp. For  , the cusp expands to an inner loop and the curve crosses itself at the origin. As
, the cusp expands to an inner loop and the curve crosses itself at the origin. As  approaches 0 the loop fills up the outer curve and, in the limit, the limaçon becomes a circle traversed twice.
approaches 0 the loop fills up the outer curve and, in the limit, the limaçon becomes a circle traversed twice.Measurement
The area enclosed by the limaçon is . When
. When  this counts the area enclosed by the inner loop twice. In this case the curve crosses the origin at angles
this counts the area enclosed by the inner loop twice. In this case the curve crosses the origin at angles  , the area enclosed by the inner loop is
, the area enclosed by the inner loop is , the area enclosed by the outer loop is
, the area enclosed by the outer loop is  , and the area between the loops is
, and the area between the loops is 
Relation to other curves
- Let P be a point and C be a circle whose center is not P. Then the envelope of those circles whose center lies on C and that pass through P is a limaçon.

- A pedalPedal curveIn the differential geometry of curves, a pedal curve is a curve derived by construction from a given curve ....
of a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is a limaçon. In fact, the pedal with respect to the origin of the circle with radius and center
and center  has polar equation
has polar equation 
- The inverse with respect to the unit circle of
 is
is  which is the equation of a conic section with eccentricity a/b and focus at the origin. Thus a limaçon can be defined as the inverse of a conic where the center of inversion is one of the foci. If the conic is a parabola then the inverse will be a cardioid, if the conic is a hyperbola then the corresponding limaçon will have an inner loop, and if the conic is an ellipse then the corresponding limaçon will have no loop.
which is the equation of a conic section with eccentricity a/b and focus at the origin. Thus a limaçon can be defined as the inverse of a conic where the center of inversion is one of the foci. If the conic is a parabola then the inverse will be a cardioid, if the conic is a hyperbola then the corresponding limaçon will have an inner loop, and if the conic is an ellipse then the corresponding limaçon will have no loop. - The conchoidConchoid (mathematics)A conchoid is a curve derived from a fixed point O, another curve, and a length d. For every line through O that intersects the given curve at A the two points on the line which are d from A are on the conchoid. The conchoid is, therefore, the cissoid of a circle with center O and the given curve...
of a circle with respect to a point on the circle is a limaçon. - A particular special case of a Cartesian ovalCartesian ovalIn geometry, a Cartesian oval, named after René Descartes, is determined as follows. Let and be fixed points in the plane, and let and denote the Euclidean distances from these points to a third variable point . Let and be arbitrary real numbers. Then the Cartesian oval is the locus of...
is a limaçon.
Additional reading
- Jane Grossman and Michael Grossman. "Dimple or no dimple", The Two-Year College Mathematics Journal, January 1982, pages 52–55.
- Howard Anton. Calculus, 2nd edition, page 708, John Wiley & Sons, 1984.
- Howard Anton. http://higheredbcs.wiley.com/legacy/college/anton/0471472441/add_material/analytic_geometry_in_calculus.pdf pp. 725 - 726.
- Howard Eves. A Survey of Geometry, Volume 2 (pages 51,56,273), Allyn and Bacon, 1965.
- Weisstein, Eric W. "Limaçon." From MathWorld--A Wolfram Web Resource.
- "Limacon of Pascal" at The MacTutor History of Mathematics archive
- "Limaçon" at www.2dcurves.com
- "Limaçons de Pascal" at Encyclopédie des Formes Mathématiques Remarquables (in French)
- "Limacon of Pascal" at Visual Dictionary of Special Plane Curves
- "Limacon of Pascal" on PlanetPTC (Mathcad)

