
Sinusoidal spiral
Encyclopedia
In geometry
, the sinusoidal spirals are a family of curves defined by the equation in polar coordinates

where a is a nonzero constant and n is a rational number other than 0. With a rotation about the origin, this can also be written

The term "spiral" is a misnomer, because they are not actually spirals, and often have a flower-like shape. Many well known curves are sinusoidal spirals including:
The curves were first studied by Colin Maclaurin
.
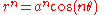
and eliminating a produces a differential equation for r and θ: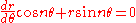 .
.
Then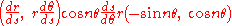
which implies that the polar tangential angle
is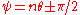
and so the tangential angle is .
.
(The sign here is positive if and
and  have the same sign and negative otherwise.)
have the same sign and negative otherwise.)
The unit tangent vector,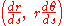 ,
,
has length one, so comparing the magnitude of the vectors on each side of the above equation gives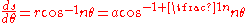 .
.
In particular, the length of a single loop when is:
is: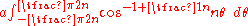
The curvature
is given by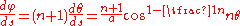 .
.
of a sinusoidal spiral with respect to a circle with center at the origin is another sinusoidal spiral whose value of n is the negative of the original curve's value of n. For example, the inverse of the lemniscate of Bernoulli is a hyperbola.
The isoptic
, pedal
and negative pedal of a sinusoidal spiral are different sinusoidal spirals.
One path of a particle moving according to a central force proportional to a power of r is a sinusoidal spiral.
When n is an integer, and n points are arranged regularly on a circle of radius a, then the set of points so that the geometric mean of the distances from the point to the n points is a is a sinusoidal spiral. In this case the sinusoidal spiral is a polynomial lemniscate
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the sinusoidal spirals are a family of curves defined by the equation in polar coordinates

where a is a nonzero constant and n is a rational number other than 0. With a rotation about the origin, this can also be written

The term "spiral" is a misnomer, because they are not actually spirals, and often have a flower-like shape. Many well known curves are sinusoidal spirals including:
- LineLine (mathematics)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
(n = −1) - CircleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
(n = 1) - Equilateral hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
(n = −2) - ParabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
(n = −1/2) - CardioidCardioidA cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp...
(n = 1/2) - Lemniscate of BernoulliLemniscate of BernoulliIn geometry, the lemniscate of Bernoulli is a plane curve defined from two given points F1 and F2, known as foci, at distance 2a from each other as the locus of points P so that PF1·PF2 = a2. The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from lemniscus, which is...
(n = 2) - Tschirnhausen cubicTschirnhausen cubicIn geometry, Tschirnhausen cubic, is a plane curve defined by the polar equationr = a\sec^3.-History:The curve was studied by von Tschirnhaus, de L'Hôpital and Catalan. It was given the name Tschirnhausen cubic in a 1900 paper by R C Archibald, though it is sometimes known as de L'Hôpital's cubic...
(n = −1/3)
The curves were first studied by Colin Maclaurin
Colin Maclaurin
Colin Maclaurin was a Scottish mathematician who made important contributions to geometry and algebra. The Maclaurin series, a special case of the Taylor series, are named after him....
.
Equations
Differentiating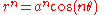
and eliminating a produces a differential equation for r and θ:
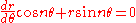 .
.Then
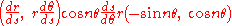
which implies that the polar tangential angle
Tangential angle
In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the x-axis. In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent...
is
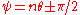
and so the tangential angle is
 .
.(The sign here is positive if
 and
and  have the same sign and negative otherwise.)
have the same sign and negative otherwise.)The unit tangent vector,
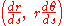 ,
,has length one, so comparing the magnitude of the vectors on each side of the above equation gives
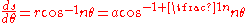 .
.In particular, the length of a single loop when
 is:
is: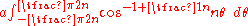
The curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
is given by
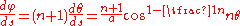 .
.Properties
The inverseInverse curve
In geometry, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·PQ = k2...
of a sinusoidal spiral with respect to a circle with center at the origin is another sinusoidal spiral whose value of n is the negative of the original curve's value of n. For example, the inverse of the lemniscate of Bernoulli is a hyperbola.
The isoptic
Isoptic
In the geometry of curves, an isoptic is the set of points for which two tangents of a given curve meet at a given angle. The orthoptic is the isoptic whose given angle is a right angle....
, pedal
Pedal curve
In the differential geometry of curves, a pedal curve is a curve derived by construction from a given curve ....
and negative pedal of a sinusoidal spiral are different sinusoidal spirals.
One path of a particle moving according to a central force proportional to a power of r is a sinusoidal spiral.
When n is an integer, and n points are arranged regularly on a circle of radius a, then the set of points so that the geometric mean of the distances from the point to the n points is a is a sinusoidal spiral. In this case the sinusoidal spiral is a polynomial lemniscate
Polynomial lemniscate
In mathematics, a polynomial lemniscate or polynomial level curve is a plane algebraic curve of degree 2n, constructed from a polynomial p with complex coefficients of degree n....

