Polynomial lemniscate
Encyclopedia
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of degree 2n, constructed from a polynomial p with complex coefficients of degree n.
For any such polynomial p and positive real number c, we may define a set of complex numbers by
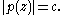This set of numbers may be equated to points in the real Cartesian plane, leading to an algebraic curve ƒ(x, y) = c2 of degree 2n, which results from expanding out 
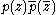in terms of z = x + iy.When p is a polynomial of degree 1 then the resulting curve is simply a circle whose center is the zero of p. When p is a polynomial of degree 2 then the curve is a Cassini oval
Cassini oval
A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
.
Erdős lemniscate
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
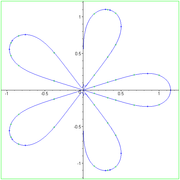
which has attracted considerable interest concerns the maximum length of a polynomial lemniscate ƒ(x, y) = 1 of degree 2n when p is monic, which Erdős conjectured was attained when p(z) = zn − 1. In the case when n = 2, the Erdős lemniscate is the Lemniscate of Bernoulli
Lemniscate of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points F1 and F2, known as foci, at distance 2a from each other as the locus of points P so that PF1·PF2 = a2. The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from lemniscus, which is...
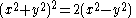
and it has been proven that this is indeed the maximal length in degree four. The Erdős lemniscate has three ordinary n-fold points, one of which is at the origin, and a genus
Geometric genus
In algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...
of (n − 1)(n − 2)/2. By inverting the Erdős lemniscate in the unit circle, one obtains a nonsingular curve of degree n.
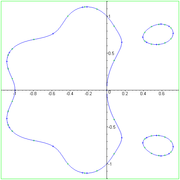
Generic polynomial lemniscate
In general, a polynomial lemniscate will not touch at the origin, and will have only two ordinary n-fold singularities, and hence a genus of (n − 1)2. As a real curve, it can have a number of disconnected components. Hence, it will not look like a lemniscate, making the name something of a misnomer.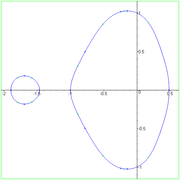
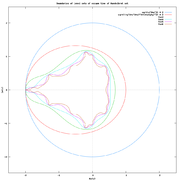
If we set p0 = z, and pn = pn−12 + z, then the corresponding polynomial lemniscates Mn defined by |pn(z)| = ER converge to the boundary of the Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
. If ER < 2 they are inside, if ER ≥ 2 they are outside of Mandelbrot set.
The Mandelbrot curves are of degree 2n+1, with two 2n-fold ordinary multiple points, and a genus of (2n − 1)2.