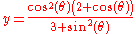
Bicorn
Encyclopedia
- For the mythical beast, see Bicorn (monster)Bicorn (monster)Bicorn is a mythological creature with two horns that has the reputation of devouring kind-hearted and devoted husbands, and is thus plump and well fed. His counterpart is the Chichevache, which devours only obedient wives and is therefore thin and starving...
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
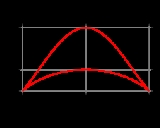
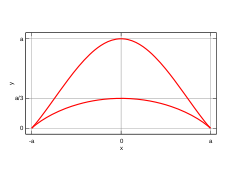
, the bicorn, also known as a cocked hat curve due to its resemblance to a bicorne
Bicorne
The bicorne or bicorn is an archaic form of hat widely adopted in the 1790s as an item of uniform by European and American military and naval officers...
, is a rational quartic curve defined by the equation
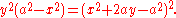
It has two cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
s and is symmetric about the y-axis.
History
In 1864, James Joseph SylvesterJames Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
studied the curve
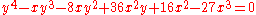
in connection with the classification of quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
s; he named the curve a bicorn because it has two cusps. This curve was further studied by Arthur Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
in 1867.
Properties
The bicorn is a plane algebraic curveAlgebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of degree four and genus
Geometric genus
In algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...
zero. It has two cusp singularities in the real plane, and a double point in the complex projective plane at x=0, z=0 . If we move x=0 and z=0 to the origin substituting and perform an imaginary rotation on x bu substituting ix/z for x and 1/z for y in the bicorn curve, we obtain
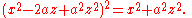
This curve, a limaçon
Limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal, is defined as a roulette formed when a circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller...
, has an ordinary double point at the origin, and two nodes in the complex plane, at x = ± i and z=1.
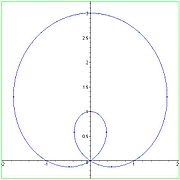
The parametric equations of a bicorn curve are:
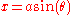 and
and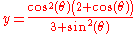 with
with