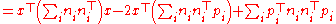In
Euclidean geometryEuclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, the
intersectionIntersection has various meanings in different contexts:*In mathematics and geometry**Intersection , the set of elements common to some collection of sets.**Line-line intersection**Line-plane intersection**Line–sphere intersection...
of a
lineThe notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
and a line can be the
empty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
,
a
pointIn geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
, or
a line. Distinguishing these cases, and finding the intersection point have use, for example, in
computer graphicsComputer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
,
motion planningMotion planning is a term used in robotics for the process of detailing a task into discrete motions....
, and
collision detectionCollision detection typically refers to the computational problem of detecting the intersection of two or more objects. While the topic is most often associated with its use in video games and other physical simulations, it also has applications in robotics...
.
The number and locations of possible intersections between two lines and the number of possible lines with no intersections (
parallelParallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
) with a given line are the distinguishing features of
Non-Euclidean geometryNon-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
.
Mathematics
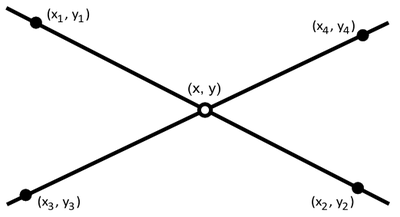
The intersection of two lines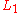
and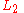
in 2 dimensional space. With line
being defined by two points
and
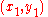, and line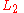
being defined by two points
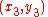and
.
The intersection
of line
and
can be defined using
determinantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s.
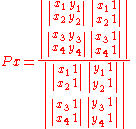
The determinants can be written out as:
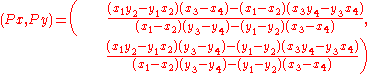
Note that the intersection point is for the infinitely long lines defined by the points, rather than the
line segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s between the points, and can produce an intersection point beyond the lengths of the line segments.
n-line intersection
In two dimensions, more than two lines almost certainly do not intersect at a single point. Similarly, in three or more dimensions, even two lines almost certainly do not intersect. However, in two or more dimensions, we can usually find a point that is mutually closest to two or more lines in a least-squares sense.
In the two-dimensional case, first, represent line
i as a point
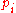on the line and a normal vector,
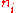perpendicular to that line. That is, if
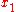and
are points on line 1, then let
and let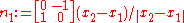
which is the unit vector along the line, rotated by 90 degrees.
Note that the distance from a point,
x to the line (
p,
n) is given by
.
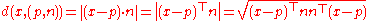And so the squared distance from a point,
x, to a line is
.
the sum of squared distances to many lines is the cost function:
This can be rearranged:
-
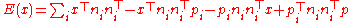
To find the minimum, we differentiate with respect to
x and set the result equal to the zero vector:
so
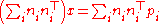
and so
.
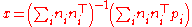This can be generalized to any number of dimensions by noting that
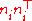is the simply the (symmetric) matrix with all eigenvalues unity except for a zero eigenvalue in the direction along the line providing a seminorm on the distance between
and another point giving the distance to the line. In any number of dimensions, if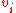
is a unit vector
along the
ith line, then
-
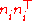becomes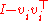 
where
I is the identity matrix, and so
-
.
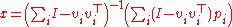See also
- Line segment intersection
In computational geometry, the line segment intersection problem supplies a list of line segments in the plane and asks us to determine whether any two of them intersect, or cross....
- Line intersection in projective space
- Distance from a point to a line
The distance from a point to a line is the shortest distance from a point to a line in Euclidean geometry. It can be calculated in the following ways.-Cartesian coordinates:...
- Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
External links