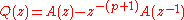Line spectral pairs
Encyclopedia
Line spectral pairs or line spectral frequencies (LSF) are used to represent linear prediction coefficients
(LPC) for transmission over a channel. LSPs have several properties (e.g. smaller sensitivity to quantization noise) that make them superior to direct quantization of LPCs. For this reason, LSPs are very useful in speech coding
.
can be decomposed into:
where P(z) corresponds to the vocal tract with the glottis
closed and Q(z) with the glottis
open.
While A(z) has complex roots anywhere within the unit circle (z-transform), P(z) and Q(z) have the very useful property of only having roots on the unit circle, hence P is a palindromic polynomial and Q an antipalindromic polynomial. So to find them we take a test point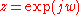
and evaluate 
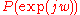and 
using a grid of points between 0 and pi. The zeros (roots) of P(z) and Q(z) also happen to be interspersed which is why we swap coefficients as we find roots. So the process of finding the LSP frequencies is basically finding the roots of two polynomials of order p + 1. The roots of P(z) and Q(z) occur in symmetrical pairs at ±w, hence the name Line Spectrum Pairs (LSPs). Because all the roots are complex and two roots are found at 0 and 
, only p/2 roots need to be found for each polynomial. The output of the LSP search thus has p roots, hence the same number of coefficients as the input LPC filter (not counting 
).
To convert back to LPCs, we need to evaluate
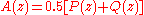
by "clocking" an impulse through it N times (order of the filter), yielding the original filter, A(z).
Includes an overview in relation to LPC.
Linear predictive coding
Linear predictive coding is a tool used mostly in audio signal processing and speech processing for representing the spectral envelope of a digital signal of speech in compressed form, using the information of a linear predictive model...
(LPC) for transmission over a channel. LSPs have several properties (e.g. smaller sensitivity to quantization noise) that make them superior to direct quantization of LPCs. For this reason, LSPs are very useful in speech coding
Speech coding
Speech coding is the application of data compression of digital audio signals containing speech. Speech coding uses speech-specific parameter estimation using audio signal processing techniques to model the speech signal, combined with generic data compression algorithms to represent the resulting...
.
Mathematical foundation
The LP polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
can be decomposed into:
where P(z) corresponds to the vocal tract with the glottis
Glottis
The glottis is defined as the combination of the vocal folds and the space in between the folds .-Function:...
closed and Q(z) with the glottis
Glottis
The glottis is defined as the combination of the vocal folds and the space in between the folds .-Function:...
open.
While A(z) has complex roots anywhere within the unit circle (z-transform), P(z) and Q(z) have the very useful property of only having roots on the unit circle, hence P is a palindromic polynomial and Q an antipalindromic polynomial. So to find them we take a test point
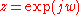and evaluate 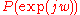and using a grid of points between 0 and pi. The zeros (roots) of P(z) and Q(z) also happen to be interspersed which is why we swap coefficients as we find roots. So the process of finding the LSP frequencies is basically finding the roots of two polynomials of order p + 1. The roots of P(z) and Q(z) occur in symmetrical pairs at ±w, hence the name Line Spectrum Pairs (LSPs). Because all the roots are complex and two roots are found at 0 and , only p/2 roots need to be found for each polynomial. The output of the LSP search thus has p roots, hence the same number of coefficients as the input LPC filter (not counting ).To convert back to LPCs, we need to evaluate
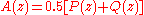
by "clocking" an impulse through it N times (order of the filter), yielding the original filter, A(z).
Properties
Line spectral pairs have several interesting and useful properties. When the roots of P(z) and Q(z) are interleaved, stability of the filter is ensured if and only if the roots are monotonically increasing. Moreover, the closer two roots are, the more resonant the filter is at the corresponding frequency. Because LSPs are not overly sensitive to quantization noise and stability is easily ensured, LSP are widely used for quantizing LPC filters. Line spectral frequencies can be interpolated.Sources
- Speex manual and source code (lsp.c)
- Tony Robinson: Speech Analysis
- "The Computation of Line Spectral Frequencies Using Chebyshev Polynomials"/ P. Kabal and R. P. Ramachandran. IEEE Trans. Acoustics, Speech, Signal Processing, vol. 34, no. 6, pp. 1419-1426, Dec. 1986.
Includes an overview in relation to LPC.
- "Line Spectral Pairs" chapter as an online excerpt (pdf) / "Digital Signal Processing - A Computer Science Perspective" (ISBN 0-471-29546-9) Jonathan Stein.