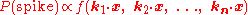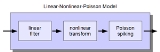
Linear-nonlinear-Poisson cascade model
Encyclopedia
The linear-nonlinear-Poisson (LNP) cascade model is a simplified functional model of neural spike responses. It has been successfully used to describe the response characteristics of neurons in early sensory pathways, especially the visual system. The LNP model is generally implicit when using reverse correlation or the spike-triggered average to characterize neural responses with white-noise stimuli.
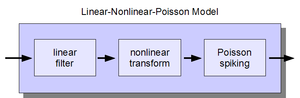 There are three stages of the LNP cascade model. The first stage consists of a linear filter, or linear receptive field
There are three stages of the LNP cascade model. The first stage consists of a linear filter, or linear receptive field
, which describes how the neuron integrates stimulus intensity over space and time. The output of this filter then passes through a nonlinear function, which gives the neuron's instantaneous spike rate as its output. Finally, the spike rate is used to generate spikes according to an inhomogeneous Poisson process
.
The linear filtering stage performs dimensionality reduction
, reducing the high-dimensional spatio-temporal stimulus space to a low-dimensional feature space, within which the neuron computes its response. The nonlinearity converts the filter output to a (non-negative) spike rate, and accounts for nonlinear phenomena such as spike threshold (or rectification) and response saturation. The Poisson spike generator converts the continuous spike rate to a series of spike times, under the assumption that the probability of a spike depends only on the instantaneous spike rate.
 denote the spatio-temporal stimulus vector at a particular instant, and
denote the spatio-temporal stimulus vector at a particular instant, and
 denote a linear filter (the neuron's linear receptive field), which is a vector with the same number of elements as
denote a linear filter (the neuron's linear receptive field), which is a vector with the same number of elements as  . Let
. Let  denote the nonlinearity, a scalar function with non-negative output. Then the LNP model specifies that, in the limit of small time bins,
denote the nonlinearity, a scalar function with non-negative output. Then the LNP model specifies that, in the limit of small time bins,
For finite-sized time bins, this can be stated precisely as the probability of observing y spikes in a single bin:
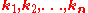 denote the set of linear filters that capture a neuron's stimulus dependence. Then the multi-filter LNP model is described by
denote the set of linear filters that capture a neuron's stimulus dependence. Then the multi-filter LNP model is described by
or
where is a matrix whose columns are the filters
is a matrix whose columns are the filters  .
.
 and the nonlinearity
and the nonlinearity  . The estimation problem (also known as the problem of neural characterization) is the problem of determining these parameters from data consisting of a time-varying stimulus and the set of observed spike times. Techniques for estimating the LNP model parameters include:
. The estimation problem (also known as the problem of neural characterization) is the problem of determining these parameters from data consisting of a time-varying stimulus and the set of observed spike times. Techniques for estimating the LNP model parameters include:

Receptive field
The receptive field of a sensory neuron is a region of space in which the presence of a stimulus will alter the firing of that neuron. Receptive fields have been identified for neurons of the auditory system, the somatosensory system, and the visual system....
, which describes how the neuron integrates stimulus intensity over space and time. The output of this filter then passes through a nonlinear function, which gives the neuron's instantaneous spike rate as its output. Finally, the spike rate is used to generate spikes according to an inhomogeneous Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
.
The linear filtering stage performs dimensionality reduction
Dimensionality reduction
In machine learning, dimension reduction is the process of reducing the number of random variables under consideration, and can be divided into feature selection and feature extraction.-Feature selection:...
, reducing the high-dimensional spatio-temporal stimulus space to a low-dimensional feature space, within which the neuron computes its response. The nonlinearity converts the filter output to a (non-negative) spike rate, and accounts for nonlinear phenomena such as spike threshold (or rectification) and response saturation. The Poisson spike generator converts the continuous spike rate to a series of spike times, under the assumption that the probability of a spike depends only on the instantaneous spike rate.
single-filter LNP
Let denote the spatio-temporal stimulus vector at a particular instant, and
denote the spatio-temporal stimulus vector at a particular instant, and denote a linear filter (the neuron's linear receptive field), which is a vector with the same number of elements as
denote a linear filter (the neuron's linear receptive field), which is a vector with the same number of elements as  . Let
. Let  denote the nonlinearity, a scalar function with non-negative output. Then the LNP model specifies that, in the limit of small time bins,
denote the nonlinearity, a scalar function with non-negative output. Then the LNP model specifies that, in the limit of small time bins,
-
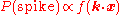 .
.
For finite-sized time bins, this can be stated precisely as the probability of observing y spikes in a single bin:
-
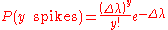
- where
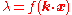 , and
, and  is the bin size.
is the bin size.
Multi-filter LNP
For neurons sensitive to multiple dimensions of the stimulus space, the linear stage of the LNP model can be generalized to a bank of linear filters, and the nonlinearity becomes a function of multiple inputs. Let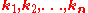 denote the set of linear filters that capture a neuron's stimulus dependence. Then the multi-filter LNP model is described by
denote the set of linear filters that capture a neuron's stimulus dependence. Then the multi-filter LNP model is described by
or
where
 is a matrix whose columns are the filters
is a matrix whose columns are the filters  .
.Estimation
The parameters of the LNP model consist of the linear filters and the nonlinearity
and the nonlinearity  . The estimation problem (also known as the problem of neural characterization) is the problem of determining these parameters from data consisting of a time-varying stimulus and the set of observed spike times. Techniques for estimating the LNP model parameters include:
. The estimation problem (also known as the problem of neural characterization) is the problem of determining these parameters from data consisting of a time-varying stimulus and the set of observed spike times. Techniques for estimating the LNP model parameters include:
- moment-based techniques, such as the spike-triggered average or spike-triggered covarianceSpike-triggered covarianceSpike-triggered covariance analysis is a tool for characterizing a neuron's response properties using the covariance of stimuli that elicit spikes from a neuron. STC is related to the spike-triggered average , and provides a complementary tool for estimating linear filters in a...
- with information-maximization or maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
techniques.
Related models
- The LNP model provides a simplified, mathematically tractable approximation to more biophysically detailed single-neuron modelsBiological neuron modelA biological neuron model is a mathematical description of the properties of nerve cells, or neurons, that is designed to accurately describe and predict biological processes...
such as the integrate-and-fire or Hodgkin–Huxley model.
- If the nonlinearity
 is a fixed invertible function, then the LNP model is a generalized linear modelGeneralized linear modelIn statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
is a fixed invertible function, then the LNP model is a generalized linear modelGeneralized linear modelIn statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
. In this case, is the inverse link function.
is the inverse link function.
- An alternative to the LNP model for neural characterization is the Volterra kernelVolterra SeriesThe Volterra series is a model for non-linear behavior similar to the Taylor series. It differs from the Taylor series in its ability to capture 'memory' effects. The Taylor series can be used to approximate the response of a nonlinear system to a given input if the output of this system depends...
or Wiener kernel series expansion, which arises in classical nonlinear systems-identification theory. These models approximate a neuron's input-output characteristics using a polynomial expansion analogous to the Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, but do not explicitly specify the spike-generation process.