.gif)
Linear space (geometry)
Encyclopedia
A linear space is a basic structure in incidence geometry. It consists of a family of subsets of a set such that the intersection of two subsets contains at most one element of the set. The elements of the set are called points and the subsets are called lines.
Linear spaces can be seen as a generalization of projective
and affine planes
, and more broadly, of 2-
block designs, where the requirement that every block contains the same number of points is dropped and the essential structural characteristic is that 2 points are incident with exactly 1 line.
The term linear space was coined by Libois in 1964, though many results about linear spaces are much older.
, for which the elements of P are called points and the elements of G are called lines. L is a linear space if the following three axioms hold:
Some authors drop (L3) when defining linear spaces. In such a situation the linear spaces complying to (L3) are considered as nontrivial and those who don't as trivial.
The following table lists all nontrivial linear spaces of five points with the usual convention, that the lines being incident with only two points are not drawn. The trivial case is simply a line through five points.
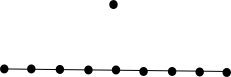
A linear space of n points containg a line being incident with n − 1 points is called a near pencil. (See pencil)
Linear spaces can be seen as a generalization of projective
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
and affine planes
Affine plane (incidence geometry)
In incidence geometry, an affine plane is a system of points and lines that satisfy the following axioms :* Any two distinct points lie on a unique line.* Given a point and line there is a unique line which contains the point and is parallel to the line...
, and more broadly, of 2-
block designs, where the requirement that every block contains the same number of points is dropped and the essential structural characteristic is that 2 points are incident with exactly 1 line.The term linear space was coined by Libois in 1964, though many results about linear spaces are much older.
Definition
Let L = (P, G, I) be an incidence structureIncidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
, for which the elements of P are called points and the elements of G are called lines. L is a linear space if the following three axioms hold:
- (L1) two points are incident with exactly one line.
- (L2) every line is incident to at least two points.
- (L3) L contains at least two lines.
Some authors drop (L3) when defining linear spaces. In such a situation the linear spaces complying to (L3) are considered as nontrivial and those who don't as trivial.
Examples
The regular Euclidean plane with its points and lines constitutes a linear space, moreover all affine and projective spaces are linear spaces as well.The following table lists all nontrivial linear spaces of five points with the usual convention, that the lines being incident with only two points are not drawn. The trivial case is simply a line through five points.
 |
 |
 |
 |
| 10 lines | 8 lines | 6 lines | 5 lines |
A linear space of n points containg a line being incident with n − 1 points is called a near pencil. (See pencil)
 |
| near pencil with 10 points |