Liouville dynamical system
Encyclopedia
In classical mechanics
, a Liouville dynamical system is an exactly soluble dynamical system
in which the kinetic energy
T and potential energy
V can be expressed in terms of the s generalized coordinates q as follows:
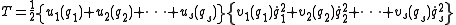
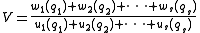
The solution of this system consists of a set of separably integrable equations
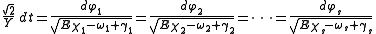
where E = T + V is the conserved energy and the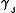
are constants. As described below, the variables have been changed from qs to φs, and the functions us and ws substituted by their counterparts χs and ωs. This solution has numerous applications, such as the orbit of a small planet about two fixed stars under the influence of Newtonian gravity
. The Liouville dynamical system is one of several things named after Joseph Liouville
, an eminent French mathematician.
, Euler's three-body problem
describes the motion of a particle in a plane under the influence of two fixed centers, each of which attract the particle with an inverse-square force
such as Newtonian gravity
or Coulomb's law
. Examples of the bicenter problem include a planet
moving around two slowly moving star
s, or an electron
moving in the electric field
of two positively charged nuclei
, such as the first ion
of the hydrogen molecule H2, namely the hydrogen molecular ion or H2+. The strength of the two attractions need not be equal; thus, the two stars may have different masses or the nuclei two different charges.
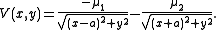
The two centers of attraction can be considered as the foci of a set of ellipses. If either center were absent, the particle would move on one of these ellipses, as a solution of the Kepler problem
. Therefore, according to Bonnet's theorem, the same ellipses are the solutions for the bicenter problem.
Introducing elliptic coordinates
,
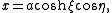
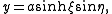
the potential energy can be written as
and the kinetic energy as
This is a Liouville dynamical system if ξ and η are taken as φ1 and φ2, respectively; thus, the function Y equals
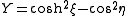
and the function W equals
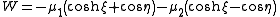
Using the general solution for a Liouville dynamical system below, one obtains
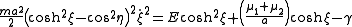
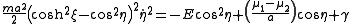
Introducing a parameter u by the formula
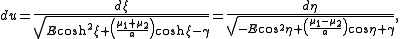
gives the parametric solution
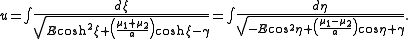
Since these are elliptic integral
s, the coordinates ξ and η can be expressed as elliptic functions of u.
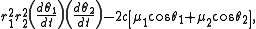
from which the problem can be solved using the method of the last multiplier.
giving the relation
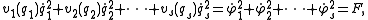
which defines a new variable F. Using the new variables, the u and w functions can be expressed by equivalent functions χ and ω. Denoting the sum of the χ functions by Y,
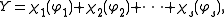
the kinetic energy can be written as
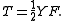
Similarly, denoting the sum of the ω functions by W
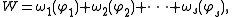
the potential energy V can be written as
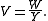
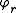is
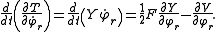
Multiplying both sides by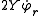
, re-arranging, and exploiting the relation 2T = YF yields the equation
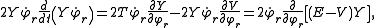
which may be written as
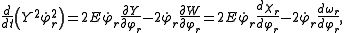
where E = T + V is the (conserved) total energy. It follows that
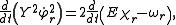
which may be integrated once to yield
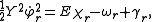
where the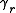
are constants of integration subject to the energy conservation
Inverting, taking the square root and separating the variables yields a set of separably integrable equations:
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, a Liouville dynamical system is an exactly soluble dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
in which the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
T and potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
V can be expressed in terms of the s generalized coordinates q as follows:
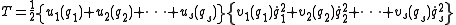
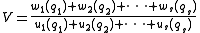
The solution of this system consists of a set of separably integrable equations
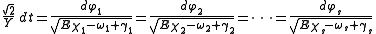
where E = T + V is the conserved energy and the
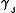are constants. As described below, the variables have been changed from qs to φs, and the functions us and ws substituted by their counterparts χs and ωs. This solution has numerous applications, such as the orbit of a small planet about two fixed stars under the influence of Newtonian gravityGravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
. The Liouville dynamical system is one of several things named after Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
, an eminent French mathematician.
Example of bicentric orbits
In classical mechanicsClassical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, Euler's three-body problem
Euler's three-body problem
In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass...
describes the motion of a particle in a plane under the influence of two fixed centers, each of which attract the particle with an inverse-square force
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
such as Newtonian gravity
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
or Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
. Examples of the bicenter problem include a planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
moving around two slowly moving star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s, or an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
moving in the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
of two positively charged nuclei
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
, such as the first ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
of the hydrogen molecule H2, namely the hydrogen molecular ion or H2+. The strength of the two attractions need not be equal; thus, the two stars may have different masses or the nuclei two different charges.
Solution
Let the fixed centers of attraction be located along the x-axis at ±a. The potential energy of the moving particle is given by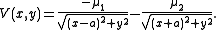The two centers of attraction can be considered as the foci of a set of ellipses. If either center were absent, the particle would move on one of these ellipses, as a solution of the Kepler problem
Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
. Therefore, according to Bonnet's theorem, the same ellipses are the solutions for the bicenter problem.
Introducing elliptic coordinates
Elliptic coordinates
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in whichthe coordinate lines are confocal ellipses and hyperbolae...
,
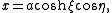
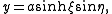
the potential energy can be written as
and the kinetic energy as
This is a Liouville dynamical system if ξ and η are taken as φ1 and φ2, respectively; thus, the function Y equals
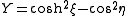
and the function W equals
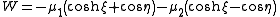
Using the general solution for a Liouville dynamical system below, one obtains
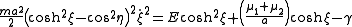
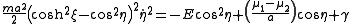
Introducing a parameter u by the formula
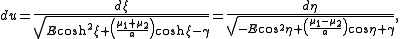
gives the parametric solution
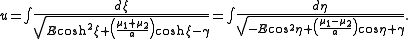
Since these are elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s, the coordinates ξ and η can be expressed as elliptic functions of u.
Constant of motion
The bicentric problem has a constant of motion, namely,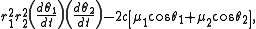from which the problem can be solved using the method of the last multiplier.
New variables
To eliminate the v functions, the variables are changed to an equivalent setgiving the relation
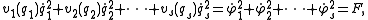
which defines a new variable F. Using the new variables, the u and w functions can be expressed by equivalent functions χ and ω. Denoting the sum of the χ functions by Y,
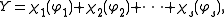
the kinetic energy can be written as
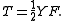
Similarly, denoting the sum of the ω functions by W
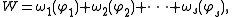
the potential energy V can be written as
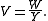
Lagrange equation
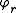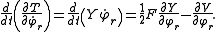
The Lagrange equation for the rth variable isMultiplying both sides by
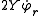, re-arranging, and exploiting the relation 2T = YF yields the equation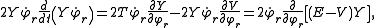which may be written as
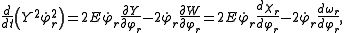
where E = T + V is the (conserved) total energy. It follows that
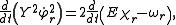
which may be integrated once to yield
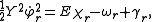
where the
are constants of integration subject to the energy conservationInverting, taking the square root and separating the variables yields a set of separably integrable equations: