Orthographic projection

Orthographic projection

Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...

s in the E₈ Coxeter plane

421

241

142

In 8-dimensional geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

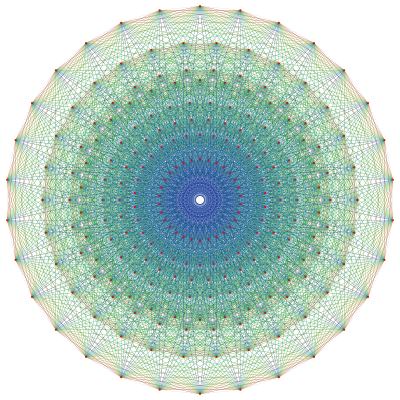
, there are 255 uniform polytopes with E₈ symmetry. The three simplest forms are the 4₂₁, 2₄₁, and 1₄₂ polytopes, composed of 240, 2160 and 17280 vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

 respectively.

These polytopes can be visualized as symmetric orthographic projection

Orthographic projection

Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...

s in Coxeter planes of the E₈ Coxeter group, and other subgroups.

Graphs

Symmetric orthographic projection

Orthographic projection

Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...

s of these 255 polytopes can be made in the E₈, E₇, E₆, D₇, D₆, D₅, D₄, D₃, A₇, A₅ Coxeter planes. A_k has [k+1] symmetry, D_k has [2(k-1)] symmetry, and E₆, E₇, E₈ have [12], [18], [30] symmetry respectively. In addition there are two other degrees of fundamental invariants, order [20] and [24] for the E₈ group that represent Coxeter planes.

11 of these 255 polytopes are each shown in 14 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.

#	Coxeter plane projections															Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Name
	E8 [30]	E7 [18]	E6 [12]	[24]	[20]	D4-E6 [6]	A3 D3 [4]	A2 D4 [6]	D5 [8]	A4 D6 [10]	D7 [12]	A6 B7 [14]	B8 [16/2]	A5   [6]	A7   [8]
1																421 (fy)
2																Rectified 421 (riffy)
3																Birectified 421 (borfy)
4																Trirectified 421 (torfy)
5																Rectified 142 (buffy)
6																Rectified 241 (robay)
7																241 (bay)
8																Truncated 241
9																Truncated 421 (tiffy)
10																142 (bif)
11																Truncated 142