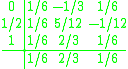List of Runge–Kutta methods
Encyclopedia
Runge–Kutta methods
are methods for the numerical solution of the ordinary differential equation
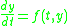
which take the form
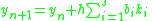
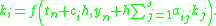
The methods listed on this page are each defined by its Butcher tableau, which puts the coefficients of the method in a table as follows:
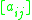is lower triangular
.
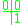
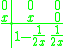
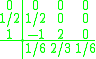
. This is done by having two methods in the tableau, one with order p and one with order p-1.
The lower-order step is given by
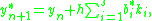
where the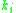
are the same as for the higher order method. Then the error is
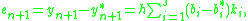
which is O(h p). The Butcher Tableau for this kind of method is extended to give the values of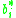
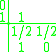
The error estimate is used to control the stepsize.
has two methods of orders 3 and 2. Its extended Butcher Tableau is:
The first row of b coefficients gives the third-order accurate solution, and the second row has order two.
has two methods of orders 5 and 4. Its extended Butcher Tableau is:
The first row of b coefficients gives the fourth-order accurate solution, and the second row has order five.
is
The first row of b coefficients gives the fifth-order accurate solution, and the second row has order four.
is
The first row of b coefficients gives the fourth-order accurate solution, and the second row has order five.
.
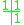
Runge–Kutta methods
In numerical analysis, the Runge–Kutta methods are an important family of implicit and explicit iterative methods for the approximation of solutions of ordinary differential equations. These techniques were developed around 1900 by the German mathematicians C. Runge and M.W. Kutta.See the article...
are methods for the numerical solution of the ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
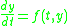
which take the form
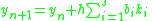
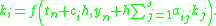
The methods listed on this page are each defined by its Butcher tableau, which puts the coefficients of the method in a table as follows:
Explicit methods
The explicit methods are those where the matrix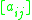 is lower triangularTriangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
.
Forward Euler
The Euler method is first order. The lack of stability and accuracy makes this popular primarily as a simple first introduction to numeric solution.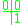Generic second-order method
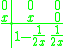
Kutta's third-order method
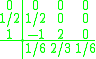
Classic fourth-order method
The "original" Runge–Kutta method.Embedded methods
The embedded methods are designed to produce an estimate of the local truncation error of a single Runge-Kutta step, and as result, allow to control the error with adaptive stepsizeAdaptive stepsize
Adaptive stepsize is a technique in numerical analysis used for many problems, but mainly for integration. It can be used for both normal integration , or the process of solving an ordinary differential equation. This article focuses on the latter...
. This is done by having two methods in the tableau, one with order p and one with order p-1.
The lower-order step is given by
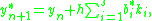
where the
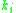are the same as for the higher order method. Then the error is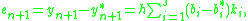which is O(h p). The Butcher Tableau for this kind of method is extended to give the values of
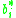
Heun–Euler
The simplest adaptive Runge–Kutta method involves combining the Heun method, which is order 2, with the Euler method, which is order 1. Its extended Butcher Tableau is: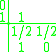The error estimate is used to control the stepsize.
Bogacki–Shampine
The Bogacki–Shampine methodBogacki–Shampine method
The Bogacki–Shampine method is a method for the numerical solution of ordinary differential equations, that was proposed by Przemyslaw Bogacki and Lawrence F. Shampine in 1989 . The Bogacki–Shampine method is a Runge–Kutta method of order three with four stages with the First Same As Last ...
has two methods of orders 3 and 2. Its extended Butcher Tableau is:
| 0 | ||||
| | 1/2 | 1/2 | |||
| | 3/4 | 0 | 3/4 | ||
| | 1 | 2/9 | 1/3 | 4/9 | |
| | | 2/9 | 1/3 | 4/9 | 0 |
| | | 7/24 | 1/4 | 1/3 | 1/8 |
The first row of b coefficients gives the third-order accurate solution, and the second row has order two.
Fehlberg
The Runge–Kutta–Fehlberg methodRunge–Kutta–Fehlberg method
In mathematics, the Runge–Kutta–Fehlberg method is an algorithm of numerical analysis for the numerical solution of ordinary differential equations. It was developed by the German mathematician Erwin Fehlberg and is based on the class of Runge–Kutta methods...
has two methods of orders 5 and 4. Its extended Butcher Tableau is:
| 0 | ||||||
| | 1/4 | 1/4 | |||||
| | 3/8 | 3/32 | 9/32 | ||||
| | 12/13 | 1932/2197 | −7200/2197 | 7296/2197 | |||
| | 1 | 439/216 | −8 | 3680/513 | −845/4104 | ||
| | 1/2 | -8/27 | 2 | −3544/2565 | 1859/4104 | −11/40 | |
| | | 25/216 | 0 | 1408/2565 | 2197/4104 | −1/5 | 0 |
| | | 16/135 | 0 | 6656/12825 | 28561/56430 | −9/50 | 2/55 |
The first row of b coefficients gives the fourth-order accurate solution, and the second row has order five.
Cash-Karp
Cash and Karp have modified Fehlberg's original idea. The extended tableau for the Cash–Karp methodCash–Karp method
In numerical analysis, the Cash–Karp method is a method for solving ordinary differential equations . It was proposed by Professor Jeff R. Cash from Imperial College London and Alan H. Karp from IBM Scientific Center. The method is a member of the Runge–Kutta family of ODE solvers...
is
| 0 | ||||||
| | 1/5 | 1/5 | |||||
| | 3/10 | 3/40 | 9/40 | ||||
| | 3/5 | 3/10 | −9/10 | 6/5 | |||
| | 1 | −11/54 | 5/2 | −70/27 | 35/27 | ||
| | 7/8 | 1631/55296 | 175/512 | 575/13824 | 44275/110592 | 253/4096 | |
| | | 37/378 | 0 | 250/621 | 125/594 | 0 | 512/1771 |
| | | 2825/27648 | 0 | 18575/48384 | 13525/55296 | 277/14336 | 1/4 |
The first row of b coefficients gives the fifth-order accurate solution, and the second row has order four.
Dormand–Prince
The extended tableau for the Dormand–Prince methodDormand–Prince method
In numerical analysis, the Dormand–Prince method, or DOPRI method, is a method for solving ordinary differential equations . The method is a member of the Runge–Kutta family of ODE solvers. More specifically, it uses six function evaluations to calculate fourth- and fifth-order accurate solutions...
is
| 0 | |||||||
| | 1/5 | 1/5 | ||||||
| | 3/10 | 3/40 | 9/40 | |||||
| | 4/5 | 44/45 | −56/15 | 32/9 | ||||
| | 8/9 | 19372/6561 | −25360/2187 | 64448/6561 | −212/729 | |||
| | 1 | 9017/3168 | −355/33 | 46732/5247 | 49/176 | −5103/18656 | ||
| | 1 | 35/384 | 0 | 500/1113 | 125/192 | −2187/6784 | 11/84 | |
| | | 5179/57600 | 0 | 7571/16695 | 393/640 | −92097/339200 | 187/2100 | 1/40 |
| | | 35/384 | 0 | 500/1113 | 125/192 | −2187/6784 | 11/84 | 0 |
The first row of b coefficients gives the fourth-order accurate solution, and the second row has order five.
Backward Euler
This method is first order. Unconditionally stable and non-oscillatory for linear diffusion problems.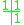Implicit midpoint
The implicit midpoint method is of second order. It is the simplest method in the class of collocation methods known as the Gauss methods. It is a symplectic integratorSymplectic integrator
In mathematics, a symplectic integrator is a numerical integration scheme for a specific group of differential equations related to classical mechanics and symplectic geometry. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations...
.
-
Lobatto methods
There are three families of Lobatto methods, called IIIA, IIIB and IIIC. These are named after Rehuel LobattoRehuel LobattoRehuel Lobatto was a Dutch mathematician. Lobatto was born in Amsterdam to a Portuguese Marrano family. As a schoolboy Lobatto already displayed remarkable talent for mathematics...
. All are implicit methods, have order 2s − 2 and they all have c1 = 0 and cs = 1. Unlike any explicit method, it's possible for these methods to have the order greater than the number of stages. Lobatto lived before the classic fourth-order method was popularized by Runge and Kutta.
Lobatto IIIA methods
The Lobatto IIIA methods are collocation methodCollocation methodIn mathematics, a collocation method is a method for the numerical solution of ordinary differential equations, partial differential equations and integral equations...
s. The second-order method is closely analogous to the Crank–Nicolson method.
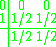
The fourth-order method is given by
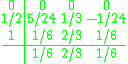
Lobatto IIIB methods
The Lobatto IIIB methods are not collocation methods, but they can be viewed as discontinuous collocation methods . The second-order method is given by
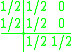
The fourth-order method is given by
Lobatto IIIC methods
The Lobatto IIIC methods also are discontinuous collocation methods. The second-order method is given by
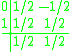
The fourth-order method is given by
