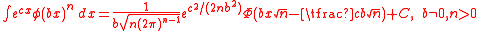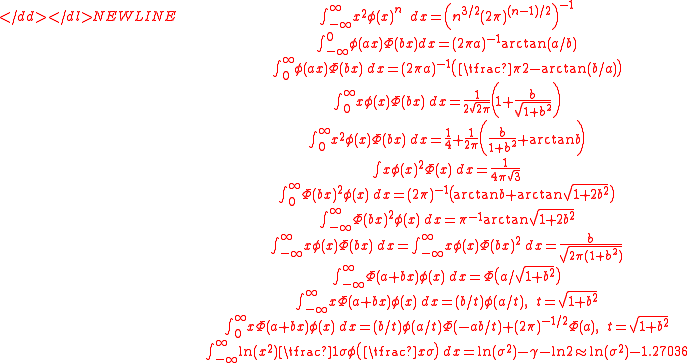List of integrals of Gaussian functions
Encyclopedia
In these expressions is the standard normal probability density function, and is the corresponding cumulative distribution function
(where erf is the error function
).
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
(where erf is the error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
).
Indefinite integrals
-

-

-
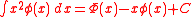
-
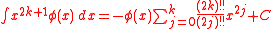 list this integral without the minus sign, which is an error. See calculation by WolframAlpha
list this integral without the minus sign, which is an error. See calculation by WolframAlpha -

-
- (in these integrals, n!! is the double factorial: for even n’s it is equal to the product of all even numbers from 2 to n, and for odd n’s it is the product of all odd numbers from 1 to n, additionally it is assumed that )
-
-
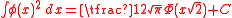
-
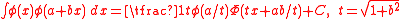 report this integral with error, see WolframAlpha
report this integral with error, see WolframAlpha -
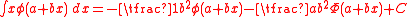
-

-
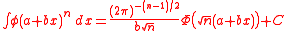
-
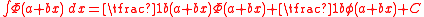
-
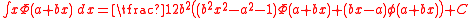
-
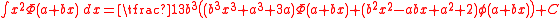
-
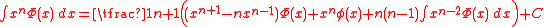
-
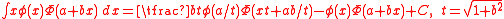
-

-