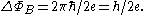Little-Parks effect
Encyclopedia
The Little–Parks effect [1] was discovered in 1962 in experiments with empty and thin-walled superconducting cylinder
s subjected to a parallel magnetic field
.
The electrical resistance
of such cylinders shows a periodic
oscillation
with the magnetic flux piercing the cylinder, the period being
The explanation provided by William A. Little and R. D. Parks is that the resistance oscillation reflects a more fundamental phenomenon, i.e. periodic oscillation of the superconducting transition critical temperature (Tc). This is the temperature at which the sample becomes superconducting.
The LP effects consists in a periodic variation of the critical temperature with the magnetic flux, which is the product of the magnetic field (coaxial) and the cross section area of the cylinder. Basically, the Tc depends on the kinetic energy of the superconducting electrons. More precisely, the critical temperature is such temperature at which the free energies of normal and superconducting electrons are equal, for a given magnetic field. To understand the periodic oscillation of the Tc, which constitutes the LP effect, one needs to understand the periodic variation of the kinetic energy (KE). The KE oscillates because the applied magnetic flux increases the kinetic energy while superconducting vortices, periodically entering the cylinder, compensate for the flux effect and reduce the KE [1]. Thus, the periodic oscillation of the kinetic energy and the related periodic oscillation of the critical temperature occur together.
The LP effect is a result of collective quantum behavior of superconducting electrons. It reflects the general fact that it is the fluxoid rather than the flux which is quantized in superconductors [2].
The Little–Parks effect can be seen as a result of the requirement that quantum physics be invariant with respect to the gauge choice
for the electromagnetic potential, of which the magnetic vector potential A forms part.
Electromagnetic theory implies that a particle with electric charge q travelling along some path P in a region with zero magnetic field
B, but non-zero A (by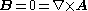
), acquires a phase shift 
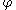, given in SI
units by
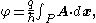
In a superconductor the electrons form a quantum superconducting condensate, called Bardeen–Cooper–Schrieffer (from the BCS theory
) condensate. In the BCS condesate all electrons behave coherently, i.e. as one particle. Thus the phase of the collective BCS wavefunction behaves under the influence of the vector potential A in the same way as the phase of a single electron. Therefore BCS condensate flowing around a closed path in a multiply connected superconducting sample acquires a phase difference Δφ determined by the magnetic flux
ΦB through the area enclosed by the path (via Stokes' theorem
and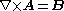
), and given by:
This phase effect is responsible for the quantized-flux
requirement and the Little–Parks effect in superconducting
loops and empty cylinders. The quantization occurs because the superconducting wave function must be single valued in a loop or an empty superconducting cylinder: its phase difference Δφ around a closed loop must be an integer multiple of 2π, with the charge q=2e for the BCS theory
electronic superconducting pairs.
If the period of the Little–Parks oscillations is 2π with respect to the superconducting phase variable, from the formula above it follows that the period with respect to the magnetic flux is the same as the magnetic flux quantum
, namely
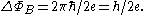
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
s subjected to a parallel magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
.
The electrical resistance
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
of such cylinders shows a periodic
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
with the magnetic flux piercing the cylinder, the period being
- h/2e = 2.07e−15 Tm2.
The explanation provided by William A. Little and R. D. Parks is that the resistance oscillation reflects a more fundamental phenomenon, i.e. periodic oscillation of the superconducting transition critical temperature (Tc). This is the temperature at which the sample becomes superconducting.
The LP effects consists in a periodic variation of the critical temperature with the magnetic flux, which is the product of the magnetic field (coaxial) and the cross section area of the cylinder. Basically, the Tc depends on the kinetic energy of the superconducting electrons. More precisely, the critical temperature is such temperature at which the free energies of normal and superconducting electrons are equal, for a given magnetic field. To understand the periodic oscillation of the Tc, which constitutes the LP effect, one needs to understand the periodic variation of the kinetic energy (KE). The KE oscillates because the applied magnetic flux increases the kinetic energy while superconducting vortices, periodically entering the cylinder, compensate for the flux effect and reduce the KE [1]. Thus, the periodic oscillation of the kinetic energy and the related periodic oscillation of the critical temperature occur together.
The LP effect is a result of collective quantum behavior of superconducting electrons. It reflects the general fact that it is the fluxoid rather than the flux which is quantized in superconductors [2].
The Little–Parks effect can be seen as a result of the requirement that quantum physics be invariant with respect to the gauge choice
Gauge fixing
In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field...
for the electromagnetic potential, of which the magnetic vector potential A forms part.
Electromagnetic theory implies that a particle with electric charge q travelling along some path P in a region with zero magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B, but non-zero A (by
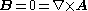), acquires a phase shift 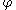, given in SISi
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units by
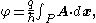
In a superconductor the electrons form a quantum superconducting condensate, called Bardeen–Cooper–Schrieffer (from the BCS theory
BCS theory
BCS theory — proposed by Bardeen, Cooper, and Schrieffer in 1957 — is the first microscopic theory of superconductivity since its discovery in 1911. The theory describes superconductivity as a microscopic effect caused by a "condensation" of pairs of electrons into a boson-like state...
) condensate. In the BCS condesate all electrons behave coherently, i.e. as one particle. Thus the phase of the collective BCS wavefunction behaves under the influence of the vector potential A in the same way as the phase of a single electron. Therefore BCS condensate flowing around a closed path in a multiply connected superconducting sample acquires a phase difference Δφ determined by the magnetic flux
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
ΦB through the area enclosed by the path (via Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
and
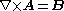), and given by:This phase effect is responsible for the quantized-flux
Magnetic flux quantum
The magnetic flux quantum Φ0 is the quantum of magnetic flux passing through a superconductor. The phenomenon of flux quantization was discovered B. S. Deaver and W. M. Fairbank and, independently, by R. Doll and M. Nabauer, in 1961...
requirement and the Little–Parks effect in superconducting
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
loops and empty cylinders. The quantization occurs because the superconducting wave function must be single valued in a loop or an empty superconducting cylinder: its phase difference Δφ around a closed loop must be an integer multiple of 2π, with the charge q=2e for the BCS theory
BCS theory
BCS theory — proposed by Bardeen, Cooper, and Schrieffer in 1957 — is the first microscopic theory of superconductivity since its discovery in 1911. The theory describes superconductivity as a microscopic effect caused by a "condensation" of pairs of electrons into a boson-like state...
electronic superconducting pairs.
If the period of the Little–Parks oscillations is 2π with respect to the superconducting phase variable, from the formula above it follows that the period with respect to the magnetic flux is the same as the magnetic flux quantum
Magnetic flux quantum
The magnetic flux quantum Φ0 is the quantum of magnetic flux passing through a superconductor. The phenomenon of flux quantization was discovered B. S. Deaver and W. M. Fairbank and, independently, by R. Doll and M. Nabauer, in 1961...
, namely