
Littlewood polynomial
Encyclopedia
In mathematics
, a Littlewood polynomial is a polynomial
all of whose coefficients are +1 or −1.
Littlewood's problem asks how large the values of such a polynomial must be on the unit circle
in the complex plane
. The answer to this would yield information about the autocorrelation
of binary sequences.
They are named for J. E. Littlewood who studied them in the 1950s.

is a Littlewood polynomial if all the . Littlewood's problem asks for constants c1 and c2 such that there are infinitely many Littlewood polynomials pn , of increasing degree n satisfying
. Littlewood's problem asks for constants c1 and c2 such that there are infinitely many Littlewood polynomials pn , of increasing degree n satisfying
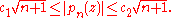
for all on the unit circle. The Rudin-Shapiro polynomials provide a sequence satisfying the upper
on the unit circle. The Rudin-Shapiro polynomials provide a sequence satisfying the upper
bound with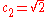 .
.
No sequence is known (as of 2008) which satisfies the lower bound.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Littlewood polynomial is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
all of whose coefficients are +1 or −1.
Littlewood's problem asks how large the values of such a polynomial must be on the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. The answer to this would yield information about the autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
of binary sequences.
They are named for J. E. Littlewood who studied them in the 1950s.
Definition
A polynomial
is a Littlewood polynomial if all the
 . Littlewood's problem asks for constants c1 and c2 such that there are infinitely many Littlewood polynomials pn , of increasing degree n satisfying
. Littlewood's problem asks for constants c1 and c2 such that there are infinitely many Littlewood polynomials pn , of increasing degree n satisfying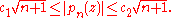
for all
 on the unit circle. The Rudin-Shapiro polynomials provide a sequence satisfying the upper
on the unit circle. The Rudin-Shapiro polynomials provide a sequence satisfying the upperbound with
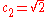 .
.No sequence is known (as of 2008) which satisfies the lower bound.

