Local nonsatiation
Encyclopedia
The property of local nonsatiation of consumer preferences states that for any bundle
of goods there is always another bundle of goods arbitrarily close that is preferred to it.
Formally if X is the consumption set, then for any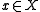
and every 
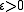, there exists a 
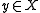such that 
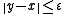and 
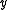is preferred to 
.
Several things to note are:
1. Local nonsatiation is implied by monotonicity of preferences
, but not vice versa. Hence it is a weaker condition.
2. There is no requirement that the preferred bundle y contain more of any good - hence, some goods can be "bads" and preferences can be non-monotone.
3. It rules out the extreme case where all goods are "bads", since then the point x = 0 would be a bliss point
.
4. The consumption set must be either unbounded or open
(in other words, it cannot be compact
). If it were compact it would necessarily have a bliss point, which local nonsatiation rules out.
Bundle
Bundle or Bundling may refer to:In marketing:* Product bundling, a marketing strategy that involves offering several products for sale as one combined product...
of goods there is always another bundle of goods arbitrarily close that is preferred to it.
Formally if X is the consumption set, then for any
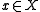and every 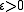, there exists a 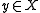such that 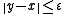and 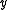is preferred to .Several things to note are:
1. Local nonsatiation is implied by monotonicity of preferences
Monotone preferences
In economics, an agent's preferences are said to be weakly monotonic if, given a consumption bundle x, the agent prefers all consumption bundles y that have more of every good. That is, y \gg x implies y\succ x. An agent's preferences are said to be strongly monotonic if, given a consumption...
, but not vice versa. Hence it is a weaker condition.
2. There is no requirement that the preferred bundle y contain more of any good - hence, some goods can be "bads" and preferences can be non-monotone.
3. It rules out the extreme case where all goods are "bads", since then the point x = 0 would be a bliss point
Bliss point
In economics, a bliss point is a quantity of consumption such that further increases would make the consumer less satisfied. Thus, it is a quantity of consumption which maximizes utility in the absence of any budget constraint. In other words, it refers to the amount of consumption that would be...
.
4. The consumption set must be either unbounded or open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
(in other words, it cannot be compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
). If it were compact it would necessarily have a bliss point, which local nonsatiation rules out.