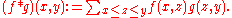In mathematics, a locally finite poset is a partially ordered set

Partially ordered set

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...

 P such that for all x, y ∈ P, the interval [x, y] consists of finitely many elements.

Given a locally finite poset P we can define its incidence algebra

Incidence algebra

In order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...

. Elements of the incidence algebra are functions ƒ that assign to each interval [x, y] of P a real number ƒ(x, y). These functions form an associative algebra

Associative algebra

In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...

 with a product defined by

(See incidence algebra

Incidence algebra

In order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...

 for more details)

In theoretical physics

Theoretical physics

Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...

 a locally finite poset is also called a causal set and has been used as a model for spacetime

Spacetime

In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...

.