
Logarithmic Schrödinger equation
Encyclopedia
In theoretical physics
, the logarithmic Schrödinger equation (sometimes abbreviated as LNSE or LogSE) is one of the nonlinear modifications of Schrödinger's equation
. It is a classical wave equation with applications to extensions of quantum mechanics
,
quantum optics
,
nuclear physics
,
transport
and diffusion
phenomena,
open quantum
systems and information theory
,
effective quantum gravity
and physical vacuum
models
and
theory of superfluidity and Bose–Einstein condensation. It is an example of an integrable model.
. In mathematics
and mathematical physics
one often uses its dimensionless form:

for the complex-valued
function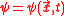 . Here
. Here  is the Laplacian with respect to the vector
is the Laplacian with respect to the vector
 .
.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the logarithmic Schrödinger equation (sometimes abbreviated as LNSE or LogSE) is one of the nonlinear modifications of Schrödinger's equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. It is a classical wave equation with applications to extensions of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
,
quantum optics
Quantum optics
Quantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...
,
nuclear physics
Nuclear physics
Nuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
,
transport
Transport
Transport or transportation is the movement of people, cattle, animals and goods from one location to another. Modes of transport include air, rail, road, water, cable, pipeline, and space. The field can be divided into infrastructure, vehicles, and operations...
and diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
phenomena,
open quantum
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
systems and information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
,
effective quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
and physical vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
models
and
theory of superfluidity and Bose–Einstein condensation. It is an example of an integrable model.
The equation
The logarithmic Schrödinger equation is the partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
. In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
one often uses its dimensionless form:

for the complex-valued
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
function
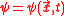 . Here
. Here  is the Laplacian with respect to the vector
is the Laplacian with respect to the vectorVector
Vector, a Latin word meaning "carrier", may refer in English to:-In computer science:*A one-dimensional array**Vector , a data type in the C++ Standard Template Library...
 .
.

