Logarithmically convex function
Encyclopedia
In mathematics
, a function
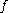defined on a convex subset
of a real vector space
and taking positive values is said to be logarithmically convex if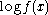
is a convex function
of
.
A logarithmically convex function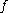
is a convex function since it is the composition
of two convex functions,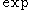
and 
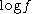. But the converse is not always true. For example 
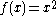is a convex function, but 
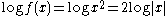is not a convex function and thus 
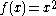is not logarithmically convex. On the other hand, 
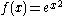is logarithmically convex since 
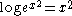is convex. A less trivial example of a logarithmically convex function is the gamma function
, if restricted to the positive reals (see also the Bohr–Mollerup theorem).
The term "superconvex" is sometimes used instead of "logarithmically convex".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
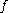defined on a convex subsetConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
of a real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
and taking positive values is said to be logarithmically convex if
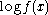is a convex functionConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
of
.A logarithmically convex function
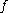is a convex function since it is the compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of two convex functions,
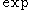and 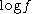. But the converse is not always true. For example 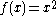is a convex function, but 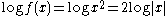is not a convex function and thus 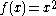is not logarithmically convex. On the other hand, 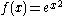is logarithmically convex since 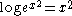is convex. A less trivial example of a logarithmically convex function is the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, if restricted to the positive reals (see also the Bohr–Mollerup theorem).
The term "superconvex" is sometimes used instead of "logarithmically convex".