Loop theorem
Encyclopedia
In mathematics, in the topology
of 3-manifold
s, the loop theorem is a generalization of Dehn's lemma
. The loop theorem was first proven by Christos Papakyriakopoulos
in 1956, along with Dehn's lemma and the Sphere theorem.
A simple and useful version of the loop theorem states that if there is a map
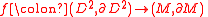
with
not nullhomotopic in 
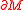, then there is an embedding with the same property.
The following version of the loop theorem, due to John Stallings, is given in the standard 3-manifold treatises (such as Hempel or Jaco):
Let
be a 3-manifold
and let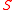
be a connected surface in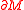
. Let 
be a normal subgroup
such that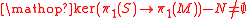
.
Let
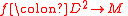
be a continuous map such that
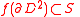
and
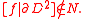
Then there exists an embedding
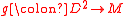
such that
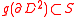
and
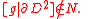
Furthermore if one starts with a map f in general position, then for any neighborhood U of the singularity set of f, we can find such a g with image lying inside the union of image of f and U.
Stalling's proof utilizes an adaptation, due to Whitehead and Shapiro, of Papakyriakopoulos' "tower construction". The "tower" refers to a special sequence of coverings designed to simplify lifts of the given map. The same tower construction was used by Papakyriakopoulos to prove the sphere theorem (3-manifolds)
, which states that a nontrivial map of a sphere into a 3-manifold implies the existence of a nontrivial embedding of a sphere. There is also a version of Dehn's lemma for minimal discs due to Meeks and S.-T. Yau, which also crucially relies on the tower construction.
A proof not utilizing the tower construction exists of the first version of the loop theorem. This was essentially done 30 years ago by Friedhelm Waldhausen
as part of his solution to the word problem for Haken manifold
s; although he recognized this gave a proof of the loop theorem, he did not write up a detailed proof. The essential ingredient of this proof is the concept of Haken hierarchy. Proofs were later written up, by Klaus Johannson, Marc Lackenby, and Iain Aitchison with Hyam Rubinstein.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s, the loop theorem is a generalization of Dehn's lemma
Dehn's lemma
In mathematics Dehn's lemmaasserts that a piecewise-linear map of a disk into a 3-manifold, with the map's singularity set in the disc's interior, implies the existence of another piecewise-linear map of the disc which is an embedding and is identical to the original on the boundary of the...
. The loop theorem was first proven by Christos Papakyriakopoulos
Christos Papakyriakopoulos
Christos Dimitriou Papakyriakopoulos, commonly known as "Papa" , was a Greek mathematician specializing in geometric topology. He worked in isolation at Athens University being awarded a Ph.D on the recommendation of Carathéodory...
in 1956, along with Dehn's lemma and the Sphere theorem.
A simple and useful version of the loop theorem states that if there is a map
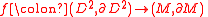
with
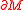not nullhomotopic in , then there is an embedding with the same property.The following version of the loop theorem, due to John Stallings, is given in the standard 3-manifold treatises (such as Hempel or Jaco):
Let
be a 3-manifold3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
and let
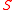
be a connected surface in
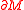. Let be a normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
such that
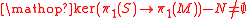.Let
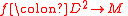
be a continuous map such that
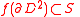
and
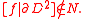
Then there exists an embedding
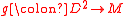
such that
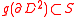
and
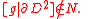
Furthermore if one starts with a map f in general position, then for any neighborhood U of the singularity set of f, we can find such a g with image lying inside the union of image of f and U.
Stalling's proof utilizes an adaptation, due to Whitehead and Shapiro, of Papakyriakopoulos' "tower construction". The "tower" refers to a special sequence of coverings designed to simplify lifts of the given map. The same tower construction was used by Papakyriakopoulos to prove the sphere theorem (3-manifolds)
Sphere theorem (3-manifolds)
In mathematics, in the topology of 3-manifolds, the sphere theorem of gives conditions for elements of the second homotopy group of a 3-manifold to be represented by embedded spheres.One example is the following:...
, which states that a nontrivial map of a sphere into a 3-manifold implies the existence of a nontrivial embedding of a sphere. There is also a version of Dehn's lemma for minimal discs due to Meeks and S.-T. Yau, which also crucially relies on the tower construction.
A proof not utilizing the tower construction exists of the first version of the loop theorem. This was essentially done 30 years ago by Friedhelm Waldhausen
Friedhelm Waldhausen
Friedhelm Waldhausen is a German mathematician known for his work in algebraic topology.-Academic life:...
as part of his solution to the word problem for Haken manifold
Haken manifold
In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...
s; although he recognized this gave a proof of the loop theorem, he did not write up a detailed proof. The essential ingredient of this proof is the concept of Haken hierarchy. Proofs were later written up, by Klaus Johannson, Marc Lackenby, and Iain Aitchison with Hyam Rubinstein.