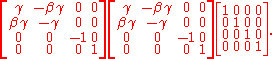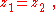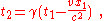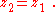Lorentz transformation under symmetric configuration
Encyclopedia
In physics
, the Lorentz transformation
converts between two different observers' measurements of space and time, where one observer is in constant motion with respect to the other.
Assume there are two observers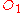 and
and 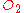 , each using their own Cartesian coordinate system
, each using their own Cartesian coordinate system
to measure space and time intervals.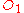 uses
uses 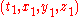 and
and  uses
uses 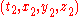 . Assume further that the coordinate systems are oriented so that the
. Assume further that the coordinate systems are oriented so that the 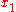 -axis and the
-axis and the 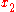 -axis overlap but in opposite directions. The
-axis overlap but in opposite directions. The  -axis is parallel to the
-axis is parallel to the 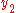 -axis but in opposite directions. The
-axis but in opposite directions. The 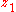 -axis is parallel to the
-axis is parallel to the 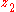 -axis and in the same direction. The relative velocity between the two observers is
-axis and in the same direction. The relative velocity between the two observers is  along the
along the 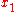 or
or 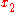 axis.
axis.  is defined as a positive number when
is defined as a positive number when 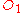 sees
sees  sliding in the direction of
sliding in the direction of 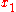 . Also assume that the origins of both coordinate systems are the same. If all this holds, then the coordinate systems are said to be in symmetric configuration.
. Also assume that the origins of both coordinate systems are the same. If all this holds, then the coordinate systems are said to be in symmetric configuration.
In this configuration, frame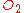 appears to
appears to 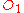 in the identical way that frame
in the identical way that frame 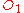 appears to
appears to 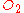 . However, in the standard configuration, if
. However, in the standard configuration, if 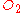 sees
sees 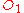 going forward then
going forward then 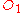 sees
sees 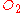 going backward. This symmetric configuration is equivalent to the [Lorentz transform#Lorentz transformation for frames in standard configuration|standard configuration]] followed by a mirror reflection of the x and y-axes. For the stationary
going backward. This symmetric configuration is equivalent to the [Lorentz transform#Lorentz transformation for frames in standard configuration|standard configuration]] followed by a mirror reflection of the x and y-axes. For the stationary  case, this reduces to only the reflections, whereas the standard form reduces to the identity transformation.
case, this reduces to only the reflections, whereas the standard form reduces to the identity transformation.
The Lorentz transformation for frames in symmetric configuration is:
where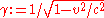 is the Lorentz factor
is the Lorentz factor
.
The inverse transformation is:
The above forward and inverse transformations are identical. This offers mathematical simplicity.
In matrix
form the forward symmetric transformation is: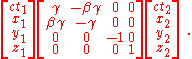
where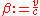 .
.
The inverse symmetric transformation is: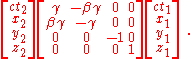
A single transformation matrix is used for both the forward and the inverse operation.
As expected: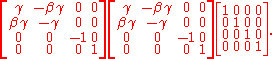
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
converts between two different observers' measurements of space and time, where one observer is in constant motion with respect to the other.
Assume there are two observers
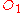 and
and 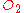 , each using their own Cartesian coordinate system
, each using their own Cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
to measure space and time intervals.
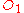 uses
uses 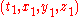 and
and  uses
uses 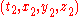 . Assume further that the coordinate systems are oriented so that the
. Assume further that the coordinate systems are oriented so that the 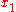 -axis and the
-axis and the 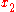 -axis overlap but in opposite directions. The
-axis overlap but in opposite directions. The  -axis is parallel to the
-axis is parallel to the 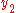 -axis but in opposite directions. The
-axis but in opposite directions. The 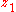 -axis is parallel to the
-axis is parallel to the 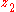 -axis and in the same direction. The relative velocity between the two observers is
-axis and in the same direction. The relative velocity between the two observers is  along the
along the 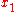 or
or 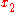 axis.
axis.  is defined as a positive number when
is defined as a positive number when 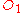 sees
sees  sliding in the direction of
sliding in the direction of 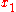 . Also assume that the origins of both coordinate systems are the same. If all this holds, then the coordinate systems are said to be in symmetric configuration.
. Also assume that the origins of both coordinate systems are the same. If all this holds, then the coordinate systems are said to be in symmetric configuration.In this configuration, frame
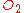 appears to
appears to 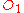 in the identical way that frame
in the identical way that frame 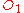 appears to
appears to 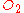 . However, in the standard configuration, if
. However, in the standard configuration, if 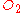 sees
sees 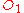 going forward then
going forward then 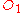 sees
sees 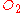 going backward. This symmetric configuration is equivalent to the [Lorentz transform#Lorentz transformation for frames in standard configuration|standard configuration]] followed by a mirror reflection of the x and y-axes. For the stationary
going backward. This symmetric configuration is equivalent to the [Lorentz transform#Lorentz transformation for frames in standard configuration|standard configuration]] followed by a mirror reflection of the x and y-axes. For the stationary  case, this reduces to only the reflections, whereas the standard form reduces to the identity transformation.
case, this reduces to only the reflections, whereas the standard form reduces to the identity transformation.The Lorentz transformation for frames in symmetric configuration is:
where
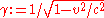 is the Lorentz factor
is the Lorentz factorLorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
.
The inverse transformation is:
The above forward and inverse transformations are identical. This offers mathematical simplicity.
In matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
form the forward symmetric transformation is:
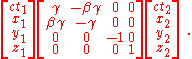
where
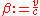 .
.The inverse symmetric transformation is:
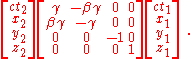
A single transformation matrix is used for both the forward and the inverse operation.
As expected: