Lovelock theory of gravity
Encyclopedia
In physics
, Lovelock's theory of gravity (often referred to as Lovelock gravity) is a generalization of Einstein's theory of general relativity
introduced by David Lovelock in 1971. It is the most general metric theory of gravity yielding conserved second order equations of motion in arbitrary number of spacetime
dimensions
. In this sense, Lovelock's theory is the natural generalization of Einstein's General Relativity to higher dimensions. In dimension three and four (
), Lovelock's theory coincides with Einstein's theory, but in higher dimension both theories are different. In fact, for 
Einstein gravity can be thought of as a particular case of Lovelock gravity since the Einstein-Hilbert action is one of several terms that constitute the Lovelock action.
The Lagrangian
of the theory is given by a sum of dimensionally extended
Euler densities, and it can be written as follows
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Lovelock's theory of gravity (often referred to as Lovelock gravity) is a generalization of Einstein's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
introduced by David Lovelock in 1971. It is the most general metric theory of gravity yielding conserved second order equations of motion in arbitrary number of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
dimensions
. In this sense, Lovelock's theory is the natural generalization of Einstein's General Relativity to higher dimensions. In dimension three and four (), Lovelock's theory coincides with Einstein's theory, but in higher dimension both theories are different. In fact, for Einstein gravity can be thought of as a particular case of Lovelock gravity since the Einstein-Hilbert action is one of several terms that constitute the Lovelock action.The Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
of the theory is given by a sum of dimensionally extended
Euler densities, and it can be written as follows
-
where
represents the Riemann tensor, and where the generalized Kronecker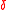 
-function is defined as the
antisymmetric product
-
Each term
in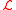 
corresponds to the dimensional
extension of the Euler density in
dimensions, so that these only
contribute to the equations of motion for
. Consequently, without
lack of generality,
in the equation above can be taken to be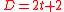 
for
even dimensions and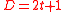
for odd dimensions.
The coupling constants
in Lagrangian 
have
dimensions of [length]
, although it is usual to normalize the
Lagrangian density in units of the Planck scalePlanck scaleIn particle physics and physical cosmology, the Planck scale is an energy scale around 1.22 × 1019 GeV at which quantum effects of gravity become strong...
. Expanding the product in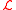 
, the Lovelock's
Lagrangian takes the form
-
where one sees that coupling
corresponds to the cosmological
constant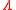
, while 
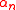with 
are coupling
constants of additional terms that represent ultraviolet corrections to
Einstein theory, involving higher order contractions of the Riemann tensor
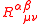. In particular, the second order term
is precisely the quadratic Gauss–Bonnet term,
which is the dimensionally extended version of the four-dimensional Euler
density.
Due to the fact that Lovelock action contains, among others, the quadratic Gauss–Bonnet
term (i.e. the four-dimensional Euler characteristicEuler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
extended to
dimensions), it is usually said that Lovelock theory resembles string theoryString theoryString theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
inspired models of gravity. This is because such quadratic term is present in the
low energy effective action of heterotic string theory, and it also appears
in six-dimensional Calabi–Yau compactifications of M-theoryM-theoryIn theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
. In the mid
1980s, a decade after Lovelock proposed his generalization of the Einstein
tensor, the physicists began to discuss the quadratic Gauss–Bonnet term of
Lovelock action within the context of string theory, with particular
attention on its property of being free of ghost about the Minkowski space.
The theory is known to be free of ghosts about other exact backgrounds as
well, e.g. about one of the branches of its spherically symmetric solution
found by Boulware and Deser in 1985. In general, Lovelock's theory
represents a very interesting scenario to study how the physics of gravity
results corrected at short distance due to the presence of higher order
curvature terms in the action, and in the mid 2000s the theory was
considered as a testing ground to investigate the effects of introducing
higher-curvature terms in the context of AdS/CFT correspondenceAdS/CFT correspondenceIn physics, the AdS/CFT correspondence , sometimes called the Maldacena duality, is the conjectured equivalence between a string theory and gravity defined on one space, and a quantum field theory without gravity defined on the conformal boundary of this space, whose dimension is lower by one or more...
.
-
-