Low basis theorem
Encyclopedia
The low basis theorem in computability theory
states that every nonempty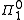
class of 
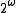(see analytical hierarchy
) contains a set of low degree
. It was first proved by Carl Jockusch
and Robert I. Soare
in 1972.
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
states that every nonempty
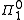class of 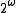(see analytical hierarchyAnalytical hierarchy
In mathematical logic and descriptive set theory, the analytical hierarchy is a higher type analogue of the arithmetical hierarchy. It thus continues the classification of sets by the formulas that define them.-The analytical hierarchy of formulas:...
) contains a set of low degree
Low (computability)
In computability theory, a Turing degree [X] is low if the Turing jump [X′] is 0′, which is the least possible degree in terms of Turing reducibility for the jump of a set. Since every set is computable from its jump, any low set is computable in 0′...
. It was first proved by Carl Jockusch
Carl Jockusch
Carl Groos Jockusch, Jr. is an American mathematician. He is a professor emeritus at the University of Illinois at Urbana-Champaign. In 1972 Jockusch and Robert I. Soare proved the Low Basis Theorem, an important result in mathematical logic with applications to recursion theory and reverse...
and Robert I. Soare
Robert I. Soare
Robert Irving Soare is an American mathematician. He is currently the Paul Snowden Russell Distinguished Service Professor of Mathematics and Computer Science at the University of Chicago, where he has been on the faculty since 1967...
in 1972.