In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the lune of Hippocrates, named after Hippocrates of Chios

Hippocrates of Chios

Hippocrates of Chios was an ancient Greek mathematician, , and astronomer, who lived c. 470 – c. 410 BCE.He was born on the isle of Chios, where he originally was a merchant. After some misadventures he went to Athens, possibly for litigation...

, is a lune

Lune (mathematics)

In geometry, a lune is either of two figures, both shaped roughly like a crescent Moon. The word "lune" derives from luna, the Latin word for Moon.-Plane geometry:...

 bounded by arcs of circles, one of which passes through the center of the other and has half the area of the other. Equivalently, it is a non-convex

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

 plane region bounded by one 180-degree circular arc and one 90-degree circular arc.

Hippocrates wanted to solve the classic problem of squaring the circle

Squaring the circle

Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...

, i.e. constructing a square by means of straightedge and compass, having the same area as a given circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

. Not until 1882, with Ferdinand von Lindemann

Ferdinand von Lindemann

Carl Louis Ferdinand von Lindemann was a German mathematician, noted for his proof, published in 1882, that π is a transcendental number, i.e., it is not a root of any polynomial with rational coefficients....

's proof of the transcendence

Transcendental number

In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...

 of π

Pi

' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...

, was that proved to be impossible.

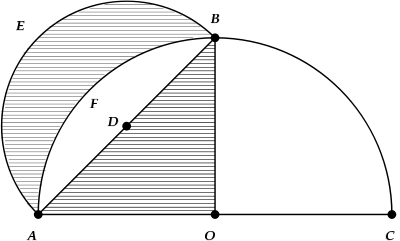
Hippocrates proved that the lune bounded by the arcs labeled E and F in the figure, has the same area as does triangle ABO.

This afforded some hope of solving the circle-squaring problem, since the lune is bounded only by arcs of circles.

The result can be proved as follows: The center of the circle on which the arc AEB lies is the point D, which is the midpoint of the hypotenuse of the isosceles right triangle ABO. Therefore the diameter AC of the larger circle ABC is √2 times the diameter of the smaller circle on which the arc AEB lies. Consequently the smaller circle has half the area of the larger circle. The semicircle bounded by the arc AEB and the diameter AB therefore has the same area as the quarter-circle bounded by the arc AFB and the two radii OA and OB. Subtracting from both sides of that equality the area of the region bounded by the arc AFB and the line AB yields the result.

(To summarize, the quarter circle AFBOA is equal in area to the semicircle AEBDA. Subtracting the crescent-shaped area, AFBDA, from both, gives triangle ABO equal in area to lune AEBFA.)

External links

• Hippocrates' Quadrature of the Lune
• Hippocrates' Squaring of the Lune at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  
• Hippocrates of Chios at the MacTutor
  MacTutor History of Mathematics archive
  The MacTutor History of Mathematics archive is a website maintained by John J. O'Connor and Edmund F. Robertson and hosted by the University of St Andrews in Scotland...