
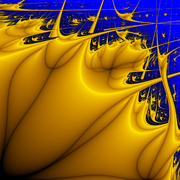
Lyapunov fractal
Encyclopedia


Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Lyapunov fractals (also known as Markus-Lyapunov fractals) are bifurcational fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s derived from an extension of the logistic map
Logistic map
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
in which the degree of the growth of the population, r, periodically switches between two values A and B.
A Lyapunov fractal is constructed by mapping the regions of stability and chaotic behaviour (measured using the Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
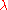 ) in the a−b plane for a given periodic sequence of as and bs. In the images, yellow corresponds to
) in the a−b plane for a given periodic sequence of as and bs. In the images, yellow corresponds to  (stability), and blue corresponds to
(stability), and blue corresponds to  (chaos).
(chaos).Properties
Lyapunov fractals are generally drawn for values of A and B in the interval . For larger values, the interval [0,1] is no longer stable, and the sequence is likely to be attracted by infinity, although convergent cycles of finite values continue to exist for some parameters. For all iteration sequences, the diagonal a = b is always the same as for the standard one parameter logistic function.
. For larger values, the interval [0,1] is no longer stable, and the sequence is likely to be attracted by infinity, although convergent cycles of finite values continue to exist for some parameters. For all iteration sequences, the diagonal a = b is always the same as for the standard one parameter logistic function.The sequence is usually started at the value 0.5, which is a critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of the iterative function. The other (even complex valued) critical points of the iterative function during one entire round are those that pass through the value 0.5 in the first round. A convergent cycle must attract at least one critical point; therefore all convergent cycles can be obtained by just shifting the iteration sequence, and keeping the starting value 0.5. In practice, shifting this sequence leads to changes in the fractal, as some branches get covered by others; notice for instance how the Lyapunov fractal for the iteration sequence AB is not perfectly symmetric with respect to a and b.
Algorithm for generating Lyapunov fractals
An algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, for computing the fractal is summarized as follows.
- Choose a string of As and Bs of any nontrivial length (e.g., AABAB).
- Construct the sequence
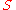 formed by successive terms in the string, repeated as many times as necessary.
formed by successive terms in the string, repeated as many times as necessary. - Choose a point
 .
. - Define the function
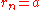 if
if 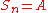 , and
, and 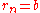 if
if  .
. - Let
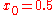 , and compute the iterates
, and compute the iterates  .
. - Compute the Lyapunov exponent:
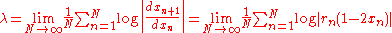
In practice,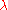 is approximated by choosing a suitably large
is approximated by choosing a suitably large  .
. - Color the point
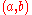 according to the value of
according to the value of  obtained.
obtained. - Repeat steps (3–7) for each point in the image plane.

