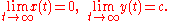Lyapunov–Malkin theorem
Encyclopedia
The Lyapunov–Malkin theorem (named for Aleksandr Lyapunov and Ioel Gilevich Malkin) is a mathematical theorem detailing nonlinear stability of systems.
s,

where, ,
,  ,
,  in an m × m matrix
in an m × m matrix
, and X(x, y), Y(x, y) represent higher order nonlinear terms. If all eigenvalues of the matrix have negative real parts, and X(x, y), Y(x, y) vanish when x = 0, then the solution x = 0, y = 0 of this system is stabile with respect to (x, y) and asymptotically stable in respect to x. If a solution (x(t), y(t)) is close enough to the solution x = 0, y = 0, then
have negative real parts, and X(x, y), Y(x, y) vanish when x = 0, then the solution x = 0, y = 0 of this system is stabile with respect to (x, y) and asymptotically stable in respect to x. If a solution (x(t), y(t)) is close enough to the solution x = 0, y = 0, then
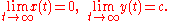
Theorem
In the system of differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s,

where,
 ,
,  ,
,  in an m × m matrix
in an m × m matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, and X(x, y), Y(x, y) represent higher order nonlinear terms. If all eigenvalues of the matrix
 have negative real parts, and X(x, y), Y(x, y) vanish when x = 0, then the solution x = 0, y = 0 of this system is stabile with respect to (x, y) and asymptotically stable in respect to x. If a solution (x(t), y(t)) is close enough to the solution x = 0, y = 0, then
have negative real parts, and X(x, y), Y(x, y) vanish when x = 0, then the solution x = 0, y = 0 of this system is stabile with respect to (x, y) and asymptotically stable in respect to x. If a solution (x(t), y(t)) is close enough to the solution x = 0, y = 0, then