
László Pyber
Encyclopedia
László Pyber is a Hungarian mathematician.
He works in combinatorics
and group theory
. He is a researcher at the Alfréd Rényi Institute of Mathematics
, Budapest.He received the title the Doctor of Science from the Hungarian Academy of Sciences
(1998). He won the Academics Prize (2007).

He works in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
. He is a researcher at the Alfréd Rényi Institute of Mathematics
Alfréd Rényi Institute of Mathematics
The Alfréd Rényi Institute of Mathematics is the research institute in mathematics of the Hungarian Academy of Sciences. It was created in 1950 by Alfréd Rényi, who directed it until his death. Since its creation, the institute has been the center of mathematical research in Hungary. It received...
, Budapest.He received the title the Doctor of Science from the Hungarian Academy of Sciences
Hungarian Academy of Sciences
The Hungarian Academy of Sciences is the most important and prestigious learned society of Hungary. Its seat is at the bank of the Danube in Budapest.-History:...
(1998). He won the Academics Prize (2007).
Main results
- He proved the conjecture of Paul ErdősPaul ErdosPaul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and Tibor GallaiTibor GallaiTibor Gallai was a Hungarian mathematician. He worked in combinatorics, especially in graph theory, and was a lifelong friend and collaborator of Paul Erdős. He was a student of Dénes König and an advisor of László Lovász...
, that the edges of any simple graph with n vertices can be covered with at most n-1 circuits and edges. - He proved the following conjecture Paul ErdősPaul ErdosPaul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
. Any graph with n vertices and its complement can be covered with n2/4+2 cliquesClique (graph theory)In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
. - He proved a clog2n bound to the size of a minimal base of a primitive permutation groupPrimitive permutation groupIn mathematics, a permutation group G acting on a set X is called primitive if G acts transitively on X and G preserves no nontrivial partition of X...
of degree n not containing An. - He gave the following estimate of the number of groups of order n. If the prime power decomposition of n is n=p1g1 ⋯ pkgk and μ=max(g1,...,gk), then the number of nonisomporphic n-element groups is at most

- ŁuczakTomasz ŁuczakTomasz Łuczak is a Polish mathematician and professor at Adam Mickiewicz University and Emory University. His main field of research is combinatorics. In particular, he analysed discrete structures, like random graphs, and their chromatic number.Łuczak earned his doctorate at Adam Mickiewicz...
and Pyber proved the following conjecture of McKayJohn McKay (mathematician)John McKay is a dual British/Canadian citizen, a mathematician at Concordia University, known for his discovery of monstrous moonshine, his joint construction of some sporadic simple groups, for the McKay conjecture in representation theory, and for the McKay correspondence relating certain...
. For every, ε>0 there is a number c such that for all sufficiently large n, c randomly chosen elements generate the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn with probability greater than 1-ε. - A result also proved by Łuczak and Pyber states that almost every element of Sn does not belong to a transitive subgroup different from Sn and An (conjectured by CameronPeter Cameron (mathematician)Peter Jephson Cameron is an Australian mathematician who works ingroup theory, combinatorics, coding theory, and model theory. He is currently Professor of Mathematics at Queen Mary, University of London....
).
- Solving a problem of subgroup growth he proved that for every nondecreasing function g(n)≤log(n) there is a residually finite groupResidually finite groupIn the mathematical field of group theory, a group G is residually finite or finitely approximable if for every nontrivial element g in G there is a homomorphism h from G to a finite group, such thath \neq 1.\,...
generated by 4 element, whose growth type is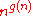 .
.
Selected papers
- L. Pyber: An Erdős-Gallai conjecture, CombinatoricaCombinatoricaCombinatorica is an international journal of mathematics, publishing papers in the fields of combinatorics and computer science. It started in 1981, with László Babai and László Lovász as the editors-in-chief with Paul Erdős as honorary editor-in-chief. The current editors-in-chief are László...
, 5(1985), 67–79. - L. Pyber: Clique covering of graphs, CombinatoricaCombinatoricaCombinatorica is an international journal of mathematics, publishing papers in the fields of combinatorics and computer science. It started in 1981, with László Babai and László Lovász as the editors-in-chief with Paul Erdős as honorary editor-in-chief. The current editors-in-chief are László...
, 6(1986), 393–398. - L. Pyber: Enumerating finite groups of given order, Annals of MathematicsAnnals of MathematicsThe Annals of Mathematics is a bimonthly mathematical journal published by Princeton University and the Institute for Advanced Study. It ranks amongst the most prestigious mathematics journals in the world by criteria such as impact factor.-History:The journal began as The Analyst in 1874 and was...
, (2), 137(1993), 203–220. - L. Pyber: On the orders of doubly transitive permutation groups, elementary estimates, J. Combin. TheoryJournal of Combinatorial TheoryThe Journal of Combinatorial Theory, Series A and Series B, are mathematical journals specializing in combinatorics and related areas. They are published by Elsevier. Series A is concerned primarily with structures, designs, and applications of combinatorics. Series B is concerned primarily with...
, (A), 62(1993), 361–366. - L. Pyber: Groups of intermediate subgroup growth and a problem of Grothendieck, Duke Math. J.Duke Mathematical JournalDuke Mathematical Journal is a peer-reviewed mathematics journal published by Duke University Press. It was established in 1935. The founding editors-in-chief were David Widder, Arthur Coble, and Joseph Miller Thomas. The first issue included a paper by Solomon Lefschetz...
, 121(2004), 169–188. - A. Jaikin-Zapirain, L. Pyber: Random generation of finite and profinite groups and group enumeration, to appear in Annals of Mathematics.
External links
- Pyber's home page.
- Pyber's nomination for Hungarian Academy of SciencesHungarian Academy of SciencesThe Hungarian Academy of Sciences is the most important and prestigious learned society of Hungary. Its seat is at the bank of the Danube in Budapest.-History:...
membership

