Primitive permutation group
Encyclopedia
In mathematics
, a permutation group
G acting on a set X is called primitive if G acts transitively on X and G preserves no nontrivial partition
of X. Otherwise, if G does preserve a nontrivial partition, G is called imprimitive.
This terminology has been introduced in his last letter by Évariste Galois
who called (in French) equation primitive an equation whose Galois group
is primitive.
In the same letter he stated also the following theorem.
If G is a primitive solvable group
acting on a finite set X, then the order of X is a power of a prime number
p, X may be identified with an affine space
over the finite field
with p elements and G acts on X as a subgroup of the affine group
.
An imprimitive permutation group is an example of an induced representation
; examples include coset
representations G/H in cases where H is not a maximal subgroup
. When H is maximal, the coset representation is primitive.
If the set X is finite, its cardinality is called the "degree" of G.
The numbers of primitive groups of small degree were stated by Robert Carmichael in 1937:
Note the large number of primitive groups of degree 16. As Carmichael notes, all of these groups, except for the symmetric
and alternating group, are subgroups of the affine group
on the 4-dimensional space over the 2-element finite field
.
While primitive permutation groups are transitive by definition, not all transitive permutation groups are primitive. The requirement that a primitive group be transitive is necessary only when X is a 2-element set; otherwise, the condition that G preserves no nontrivial partition implies that G is transitive.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
G acting on a set X is called primitive if G acts transitively on X and G preserves no nontrivial partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of X. Otherwise, if G does preserve a nontrivial partition, G is called imprimitive.
This terminology has been introduced in his last letter by Évariste Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
who called (in French) equation primitive an equation whose Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
is primitive.
In the same letter he stated also the following theorem.
If G is a primitive solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
acting on a finite set X, then the order of X is a power of a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, X may be identified with an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with p elements and G acts on X as a subgroup of the affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
.
An imprimitive permutation group is an example of an induced representation
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
; examples include coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
representations G/H in cases where H is not a maximal subgroup
Maximal subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
. When H is maximal, the coset representation is primitive.
If the set X is finite, its cardinality is called the "degree" of G.
The numbers of primitive groups of small degree were stated by Robert Carmichael in 1937:
| Degree | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | OEIS |
| Number | 1 | 2 | 2 | 5 | 4 | 7 | 7 | 11 | 9 | 8 | 6 | 9 | 4 | 6 | 22 | 10 | 4 | 8 | 4 |
Note the large number of primitive groups of degree 16. As Carmichael notes, all of these groups, except for the symmetric
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
and alternating group, are subgroups of the affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
on the 4-dimensional space over the 2-element finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
.
While primitive permutation groups are transitive by definition, not all transitive permutation groups are primitive. The requirement that a primitive group be transitive is necessary only when X is a 2-element set; otherwise, the condition that G preserves no nontrivial partition implies that G is transitive.
Examples
- Consider the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
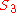acting on the set 
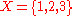and the permutation
-
.
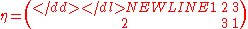The group generated by
and 
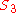are both primitive.
- Now consider the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
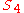acting on the set 
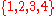and the permutation
-
.
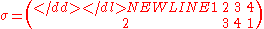The group generated by
is not primitive, since the partition 
where 
and 
is preserved under 
, i.e. 
and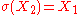 
.
- Every transitive group of prime degree is primitive
- Every simple groupSimple groupIn mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
is primitive. In particular the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
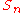is primitive for every n>1 and the alternating group 
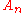is primitive for every n>2.
- Now consider the symmetric group