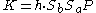MQV
Encyclopedia
MQV is an authenticated
protocol for key agreement based on the Diffie–Hellman scheme. Like other authenticated Diffie-Hellman schemes, MQV provides protection against an active attacker. The protocol can be modified to work in an arbitrary finite group
, and, in particular, elliptic curve
groups, where it is known as elliptic curve MQV (ECMQV).
MQV was initially proposed by Menezes
, Qu and Vanstone
in 1995. It was modified with Law and Solinas in 1998. There are one-, two- and three-pass variants.
MQV is incorporated in the public-key standard IEEE P1363
.
Some variants of MQV are claimed in patents assigned to Certicom http://www.certicom.com/index.php?action=ip,protocol.
MQV has some weaknesses that were fixed by HMQV in 2005 http://eprint.iacr.org/2005/176; see http://eprint.iacr.org/2005/205, http://www.ams.org/notices/200708/tx070800972p.pdf, http://www.ams.org/notices/200711/tx071101454p.pdf for an alternative viewpoint.
ECMQV has been dropped from the National Security Agency's Suite B
set of cryptographic standards.
Both MQV and HMQV have weaknesses, that are fixed in the FHMQV protocol (see http://eprint.iacr.org/2009/408)
In the following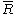 has the following meaning. Let
has the following meaning. Let 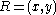 be a point on an elliptic curve. Then
be a point on an elliptic curve. Then 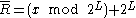 where
where 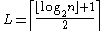 and n is the order of the used generator point P. So
and n is the order of the used generator point P. So 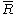 are the first L bits of the x coordinate of R.
are the first L bits of the x coordinate of R.
Note: for the algorithm to be secure some checks have to be performed. See Hankerson et al.
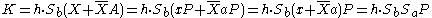 .
.
Alice calculates:
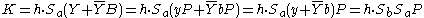 .
.
So the keys K are indeed the same with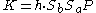
Authentication
Authentication is the act of confirming the truth of an attribute of a datum or entity...
protocol for key agreement based on the Diffie–Hellman scheme. Like other authenticated Diffie-Hellman schemes, MQV provides protection against an active attacker. The protocol can be modified to work in an arbitrary finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
, and, in particular, elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
groups, where it is known as elliptic curve MQV (ECMQV).
MQV was initially proposed by Menezes
Alfred Menezes
Alfred Menezes is co-author of several books on cryptography, most notably the Handbook of Applied Cryptography.Menezes is a professor in the Department of Combinatorics & Optimization at the University of Waterloo. He is also the Managing Director of the Centre for Applied Cryptographic...
, Qu and Vanstone
Scott Vanstone
Scott A. Vanstone is a cryptographer who co-authored the Handbook of Applied Cryptography. He is currently on faculty at the University of Waterloo's Faculty of Mathematics and a member of the school's Centre for Applied Cryptographic Research. He is also the founder of Certicom. In 1998, he was...
in 1995. It was modified with Law and Solinas in 1998. There are one-, two- and three-pass variants.
MQV is incorporated in the public-key standard IEEE P1363
IEEE P1363
IEEE P1363 is an Institute of Electrical and Electronics Engineers standardization project for public-key cryptography. It includes specifications for:* Traditional public-key cryptography...
.
Some variants of MQV are claimed in patents assigned to Certicom http://www.certicom.com/index.php?action=ip,protocol.
MQV has some weaknesses that were fixed by HMQV in 2005 http://eprint.iacr.org/2005/176; see http://eprint.iacr.org/2005/205, http://www.ams.org/notices/200708/tx070800972p.pdf, http://www.ams.org/notices/200711/tx071101454p.pdf for an alternative viewpoint.
ECMQV has been dropped from the National Security Agency's Suite B
NSA Suite B
Suite B is a set of cryptographic algorithms promulgated by the National Security Agency as part of its Cryptographic Modernization Program. It is to serve as an interoperable cryptographic base for both unclassified information and most classified information. Suite B was announced on 16...
set of cryptographic standards.
Both MQV and HMQV have weaknesses, that are fixed in the FHMQV protocol (see http://eprint.iacr.org/2009/408)
Description
Alice has a key pair (A,a) with A her public key and a her private key and Bob has the key pair (B,b) with B his public key and b his private key.In the following
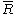 has the following meaning. Let
has the following meaning. Let 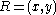 be a point on an elliptic curve. Then
be a point on an elliptic curve. Then 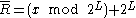 where
where 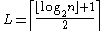 and n is the order of the used generator point P. So
and n is the order of the used generator point P. So 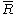 are the first L bits of the x coordinate of R.
are the first L bits of the x coordinate of R.| Step | Operation |
|---|---|
| 1 | Alice generates a key pair (X,x) by generating randomly x and calculating X=xP with P a point on an elliptic curve. |
| 2 | Bob generates a key pair (Y,y) in the same way as Alice. |
| 3 | Now, Alice calculates 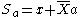 and sends X to Bob. and sends X to Bob. |
| 4 | Bob calculates 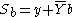 and sends Y to Alice. and sends Y to Alice. |
| 5 | Alice calculates 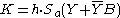 and Bob calculates and Bob calculates 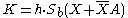 where h is the cofactor (see Elliptic curve cryptography#Domain parameters). where h is the cofactor (see Elliptic curve cryptography#Domain parameters). |
| 6 | The communication of secret 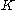 was successful. A key for a symmetric-key algorithm was successful. A key for a symmetric-key algorithmSymmetric-key algorithm Symmetric-key algorithms are a class of algorithms for cryptography that use trivially related, often identical, cryptographic keys for both encryption of plaintext and decryption of ciphertext. The encryption key is trivially related to the decryption key, in that they may be identical or there is... can be derived from K. |
Note: for the algorithm to be secure some checks have to be performed. See Hankerson et al.
Correctness
Bob calculates: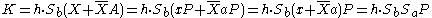 .
.Alice calculates:
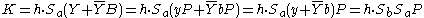 .
.So the keys K are indeed the same with