MV-algebra
Encyclopedia
In abstract algebra
, a branch of pure mathematics
, an MV-algebra is an algebraic structure
with a binary operation
, a unary operation
, and the constant 
, satisfying certain axioms. MV-algebras are models
of Łukasiewicz logic; the letters MV refer to many-valued logic of Łukasiewicz.
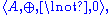consisting of
which satisfies the following identities
:
By virtue of the first three axioms,
is a commutative monoid
. Being defined by identities, MV-algebras form a variety
of algebras. The variety of MV-algebras is a subvariety of the variety of BL-algebras and contains all Boolean algebras.
An MV-algebra can equivalently be defined (Hájek 1998) as a prelinear commutative bounded integral residuated lattice
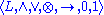satisfying the additional identity 
with operations 
and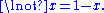 
In mathematical fuzzy logic, this MV-algebra is called the standard MV-algebra, as it forms the standard real-valued semantics of Łukasiewicz logic.
The trivial MV-algebra has the only element 0 and the operations defined in the only possible way,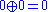
and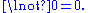 
The two-element MV-algebra is actually the two-element Boolean algebra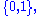
with 
coinciding with Boolean disjunction and 
with Boolean negation.
Other finite linearly ordered MV-algebras are obtained by restricting the universe and operations of the standard MV-algebra to the set of
equidistant real numbers between 0 and 1 (both included), that is, the set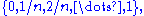 
which is closed under the operations 
and 
of the standard MV-algebra.
Another important example is Chang's MV-algebra, consisting just of infinitesimals (with the order type
ω) and their co-infinitesimals.
of Łukasiewicz logic, as described below.
Given an MV-algebra A, an A-valuation
is a homomorphism
from the algebra of propositional formula
s (in the language consisting of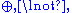
and 0) into A. Formulas mapped to 1 (or 
0) for all A-valuations are called A-tautologies
. If the standard MV-algebra over [0,1] is employed, the set of all [0,1]-tautologies determines so-called infinite-valued Łukasiewicz logic.
Chang's (1958, 1959) completeness theorem states that any MV-algebra equation holding in the standard MV-algebra over the interval [0,1] will hold in every MV-algebra. Algebraically, this means that the standard MV-algebra generates the variety of all MV-algebras. Equivalently, Chang's completeness theorem says that MV-algebras characterize infinite-valued Łukasiewicz logic, defined as the set of [0,1]-tautologies.
The way the [0,1] MV-algebra characterizes all possible MV-algebras parallels the well-known fact that identities holding in the two-element Boolean algebra hold in all possible Boolean algebras. Moreover, MV-algebras characterize infinite-valued Łukasiewicz logic in a manner analogous to the way that Boolean algebras characterize classical bivalent logic (see Lindenbaum-Tarski algebra).
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a branch of pure mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an MV-algebra is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
with a binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
, a unary operationUnary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
, and the constant , satisfying certain axioms. MV-algebras are modelsModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of Łukasiewicz logic; the letters MV refer to many-valued logic of Łukasiewicz.
Definitions
An MV-algebra is an algebraic structureAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
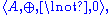consisting of
- a non-emptyEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
set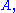
- a binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
on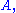 
- a unary operationUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
on 
and - a constant
denoting a fixed element of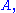 
which satisfies the following identities
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
:
-
-
-
-
-
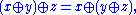
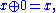
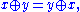
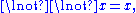
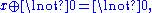and -
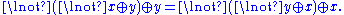
By virtue of the first three axioms,
is a commutative monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. Being defined by identities, MV-algebras form a variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
of algebras. The variety of MV-algebras is a subvariety of the variety of BL-algebras and contains all Boolean algebras.
An MV-algebra can equivalently be defined (Hájek 1998) as a prelinear commutative bounded integral residuated lattice
Residuated lattice
In abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y loosely analogous to division or implication when x•y is viewed as multiplication or conjunction respectively...
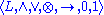satisfying the additional identity Examples of MV-algebras
A simple numerical example is with operations and 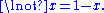In mathematical fuzzy logic, this MV-algebra is called the standard MV-algebra, as it forms the standard real-valued semantics of Łukasiewicz logic.The trivial MV-algebra has the only element 0 and the operations defined in the only possible way,
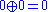and 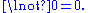The two-element MV-algebra is actually the two-element Boolean algebra
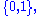with coinciding with Boolean disjunction and with Boolean negation.Other finite linearly ordered MV-algebras are obtained by restricting the universe and operations of the standard MV-algebra to the set of
equidistant real numbers between 0 and 1 (both included), that is, the set 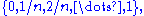which is closed under the operations and of the standard MV-algebra.Another important example is Chang's MV-algebra, consisting just of infinitesimals (with the order type
Order type
In mathematics, especially in set theory, two ordered sets X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection f: X → Y such that both f and its inverse are monotone...
ω) and their co-infinitesimals.
Relation to Łukasiewicz logic
Chang devised MV-algebras to study many-valued logics, introduced by Jan Łukasiewicz in 1920. In particular, MV-algebras form the algebraic semanticsAlgebraic semantics
An programming language theory, the algebraic semantics of a programming language is a form of axiomatic semantics based on algebraic laws for describing and reasoning about program semantics in a formal manner....
of Łukasiewicz logic, as described below.
Given an MV-algebra A, an A-valuation
Valuation (logic)
In logic and model theory, a valuation can be:*In propositional logic, an assignment of truth values to propositional variables, with a corresponding assignment of truth values to all propositional formulas with those variables....
is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from the algebra of propositional formula
Propositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
s (in the language consisting of
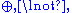and 0) into A. Formulas mapped to 1 (or 0) for all A-valuations are called A-tautologiesTautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
. If the standard MV-algebra over [0,1] is employed, the set of all [0,1]-tautologies determines so-called infinite-valued Łukasiewicz logic.
Chang's (1958, 1959) completeness theorem states that any MV-algebra equation holding in the standard MV-algebra over the interval [0,1] will hold in every MV-algebra. Algebraically, this means that the standard MV-algebra generates the variety of all MV-algebras. Equivalently, Chang's completeness theorem says that MV-algebras characterize infinite-valued Łukasiewicz logic, defined as the set of [0,1]-tautologies.
The way the [0,1] MV-algebra characterizes all possible MV-algebras parallels the well-known fact that identities holding in the two-element Boolean algebra hold in all possible Boolean algebras. Moreover, MV-algebras characterize infinite-valued Łukasiewicz logic in a manner analogous to the way that Boolean algebras characterize classical bivalent logic (see Lindenbaum-Tarski algebra).
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: " Many-valued logic" -- by Siegfried GottwaldSiegfried GottwaldSiegfried Johannes Gottwald is a German mathematician, logician and historian of science.- Life and work :...
.