
Magic number (sports)
Encyclopedia
In certain sports, a magic number is a number used to indicate how close a front-running team is to clinching a season title. It represents the total of additional wins by the front-running team or additional losses (or any combination thereof) by the rival team after which it is mathematically impossible for the rival team to capture the title in the remaining games. This assumes that each game results in a win or a loss, but not a tie
. Teams other than the front-running team have what is called an elimination number (or "tragic number") (often abbreviated E#). This number represents the number of wins by the leading team or losses by the trailing team which will eliminate the trailing team. The elimination number for the second place team is exactly the magic number for the leading team.
The magic number is calculated as G + 1 − WA − LB, where
For example, in Major League Baseball
there are 162 games in a season. Suppose the top of the division
standings late in the season are as follows:
Then the magic number for Team A to win the division is 162 + 1 − 96 − 62 = 5.
Any combination of wins by Team A and losses by Team B totaling to 5 makes it impossible for Team B to win the division title.
The "+1" in the formula serves the purpose of eliminating ties; without it, if the magic number were to decrease to zero and stay there, the two teams in question would wind up with identical records. If circumstances dictate that the front-running team would win the tiebreaker regardless of any future results, then the additional constant 1 can be eliminated. For example, the NBA
uses complicated formulae for breaking ties, using several other statistics of merit besides overall win/loss record; however the first tiebreaker between two teams is their head-to-head record; if the frontrunning team has already clinched the better head-to-head record, then the +1 is unnecessary.
The magic number can also be calculated as WB + GRB - WA + 1, where
This second formula basically says: Assume Team B wins every remaining game. Calculate how many games team A needs to win to surpass team B's maximum total by 1. Using the example above and with the same 162-game season, team B has 7 games remaining.
The magic number for Team A to win the division is still "5": 93 + 7 − 96 + 1 = 5.
Team B can win as many as 100 games. If Team A wins 101, Team B is eliminated. The magic number would decrease with a Team A win and would also decrease with a Team B loss, as its maximum win total would decrease by one.
A variation of the above looks at the relation between the losses of the two teams. The magic number can be calculated as LA + GRA - LB + 1, where
This third formula basically says: Assume Team A loses every remaining game. Calculate how many games team B needs to lose to surpass team A's maximum total by 1. Using the example above and with the same 162-game season, team A has 8 games remaining.
The magic number for Team A to win the division is still "5": 58 + 8 − 62 + 1 = 5. As you can see, the magic number is the same whether calculating it based on potential wins of the leader or potential losses of the trailing team. Indeed, mathematical proofs will show that the three formulas presented here are mathematically equivalent.
Team A can lose as many as 66 games. If Team B loses 67, Team B is eliminated. Once again, the magic number would decrease with a Team A win and would also decrease with a Team B loss.
In some sports, ties are broken by an additional one-game playoff
(s) between the teams involved. When a team gets to the point where its magic number is 1, it is said to have "clinched a tie" for the division or the wild card. However, if they end the season tied with another team, and only one is eligible for the playoffs, the extra playoff game will erase that "clinching" for the team that loses the playoff game.
By convention, the magic number typically is used to describe the first place team only, relative to the teams it leads. However, the same mathematical formulas could be applied to any team, teams that are tied for the lead, as well as teams that trail. In these cases, a team that is not in first place will depend on the leading team to lose some games so that it may catch up, so the magic number will be larger than the number of games remaining. Ultimately, for teams that are no longer in contention, their magic number would be larger than their remaining games + the remaining games for the first place team — which would be impossible to overcome.
If Team C were to win all three remaining games, it would finish at 98-64, and if both Teams A and B were to lose their three remaining games, they would finish at 97-65, which would make Team C the division winner. However if Teams A and B are playing against each other in the final weekend (in a 3 game series), it would be impossible for both teams to lose the three remaining games. One of them will win at least two games and thereby clinch the division title with a record of either 100-62 or 99-63. The more direct consequence of this situation is that it is also not possible for Teams A and B to finish in a tie with each other, and Team C can't win the division.
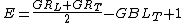 ,
,
where GR means Games Remaining, GBL means Games Behind Leader, L means Leader and T means Trailer.
Refer back to the example presented above. The elimination number for Team B is once again "5":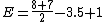 .
.
It is necessary to use this method if the teams play different numbers of games in the full season, for instance due to cancellations or ties that will not be replayed. Note that this algorithm also is limited by the aforementioned subtleties.
Tie (draw)
To tie or draw is to finish a competition with identical or inconclusive results. The word "tie" is usually used in North America for sports such as American football. "Draw" is usually used in the United Kingdom, Ireland and the Commonwealth of Nations and it is usually used for sports such as...
. Teams other than the front-running team have what is called an elimination number (or "tragic number") (often abbreviated E#). This number represents the number of wins by the leading team or losses by the trailing team which will eliminate the trailing team. The elimination number for the second place team is exactly the magic number for the leading team.
The magic number is calculated as G + 1 − WA − LB, where
- G is the total number of games in the season
- WA is the number of wins that Team A has in the season
- LB is the number of losses that Team B has in the season
For example, in Major League Baseball
Major League Baseball
Major League Baseball is the highest level of professional baseball in the United States and Canada, consisting of teams that play in the National League and the American League...
there are 162 games in a season. Suppose the top of the division
Division (sport)
In sports, a division is a group of teams who compete against each other for a championship.-League system:In sports using a league system , a division consists a group of teams who play a sport at a similar competitive level...
standings late in the season are as follows:
| Team | Wins | Losses |
| A | 96 | 58 |
| B | 93 | 62 |
Then the magic number for Team A to win the division is 162 + 1 − 96 − 62 = 5.
Any combination of wins by Team A and losses by Team B totaling to 5 makes it impossible for Team B to win the division title.
The "+1" in the formula serves the purpose of eliminating ties; without it, if the magic number were to decrease to zero and stay there, the two teams in question would wind up with identical records. If circumstances dictate that the front-running team would win the tiebreaker regardless of any future results, then the additional constant 1 can be eliminated. For example, the NBA
National Basketball Association
The National Basketball Association is the pre-eminent men's professional basketball league in North America. It consists of thirty franchised member clubs, of which twenty-nine are located in the United States and one in Canada...
uses complicated formulae for breaking ties, using several other statistics of merit besides overall win/loss record; however the first tiebreaker between two teams is their head-to-head record; if the frontrunning team has already clinched the better head-to-head record, then the +1 is unnecessary.
The magic number can also be calculated as WB + GRB - WA + 1, where
- WB is the number of wins that Team B has in the season
- GRB is the number of games remaining for Team B in the season
- WA is the number of wins that Team A has in the season
This second formula basically says: Assume Team B wins every remaining game. Calculate how many games team A needs to win to surpass team B's maximum total by 1. Using the example above and with the same 162-game season, team B has 7 games remaining.
The magic number for Team A to win the division is still "5": 93 + 7 − 96 + 1 = 5.
Team B can win as many as 100 games. If Team A wins 101, Team B is eliminated. The magic number would decrease with a Team A win and would also decrease with a Team B loss, as its maximum win total would decrease by one.
A variation of the above looks at the relation between the losses of the two teams. The magic number can be calculated as LA + GRA - LB + 1, where
- LA is the number of losses that Team A has in the season
- GRA is the number of games remaining for Team A in the season
- LB is the number of losses that Team B has in the season
This third formula basically says: Assume Team A loses every remaining game. Calculate how many games team B needs to lose to surpass team A's maximum total by 1. Using the example above and with the same 162-game season, team A has 8 games remaining.
The magic number for Team A to win the division is still "5": 58 + 8 − 62 + 1 = 5. As you can see, the magic number is the same whether calculating it based on potential wins of the leader or potential losses of the trailing team. Indeed, mathematical proofs will show that the three formulas presented here are mathematically equivalent.
Team A can lose as many as 66 games. If Team B loses 67, Team B is eliminated. Once again, the magic number would decrease with a Team A win and would also decrease with a Team B loss.
In some sports, ties are broken by an additional one-game playoff
One-game playoff
A one-game playoff, sometimes known as a pennant playoff or play-in game, is a tiebreaker in certain sports—usually but not always professional—to determine which of two teams, tied in the final standings, will qualify for a post-season tournament...
(s) between the teams involved. When a team gets to the point where its magic number is 1, it is said to have "clinched a tie" for the division or the wild card. However, if they end the season tied with another team, and only one is eligible for the playoffs, the extra playoff game will erase that "clinching" for the team that loses the playoff game.
By convention, the magic number typically is used to describe the first place team only, relative to the teams it leads. However, the same mathematical formulas could be applied to any team, teams that are tied for the lead, as well as teams that trail. In these cases, a team that is not in first place will depend on the leading team to lose some games so that it may catch up, so the magic number will be larger than the number of games remaining. Ultimately, for teams that are no longer in contention, their magic number would be larger than their remaining games + the remaining games for the first place team — which would be impossible to overcome.
Derivation
The formula for the magic number is derived straightforwardly as follows. As before, at some particular point in the season let Team A have WA wins and LA losses. Suppose that at some later time, Team A has wA additional wins and lA additional losses, and define similarly WB, LB, wB, lB for Team B. The total number of wins that Team B needs to make up is thus given by (WA + wA) − (WB + wB). Team A clinches when this number exceeds the number of games Team B has remaining, since at that point Team B cannot make up the deficit even if Team A fails to win any more games. If there are a total of G games in the season, then the number of games remaining for Team B is given by G − (WB + wB + LB + lB). Thus the condition for Team A to clinch is that (WA + wA) − (WB + wB) = 1 + G − (WB + wB + LB + lB). Canceling the common terms, we obtain wA + lB = G + 1 − WA − LB, which establishes the magic number formula.Subtlety
Sometimes a team can appear to have a mathematical chance to win even though they have actually been eliminated already, due to scheduling. In this Major League Baseball scenario, there are three games remaining in the season. Teams A, B and C are assumed to be eligible only for the division championship; another team with a better record in another division has already clinched the one available "wild card" spot:| Team | Wins | Losses |
| A | 97 | 62 |
| B | 97 | 62 |
| C | 95 | 64 |
If Team C were to win all three remaining games, it would finish at 98-64, and if both Teams A and B were to lose their three remaining games, they would finish at 97-65, which would make Team C the division winner. However if Teams A and B are playing against each other in the final weekend (in a 3 game series), it would be impossible for both teams to lose the three remaining games. One of them will win at least two games and thereby clinch the division title with a record of either 100-62 or 99-63. The more direct consequence of this situation is that it is also not possible for Teams A and B to finish in a tie with each other, and Team C can't win the division.
Alternative Method
Another method can be used to determine the Elimination Number which uses only the Games Remaining and Games Behind Leader statistics, as follows: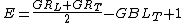 ,
,where GR means Games Remaining, GBL means Games Behind Leader, L means Leader and T means Trailer.
Refer back to the example presented above. The elimination number for Team B is once again "5":
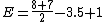 .
.It is necessary to use this method if the teams play different numbers of games in the full season, for instance due to cancellations or ties that will not be replayed. Note that this algorithm also is limited by the aforementioned subtleties.
External links
- Comparison of several equivalent formulas
- RIOT an operations research approach applied to Major League Baseball

