
Majority logic decoding
Encyclopedia
In error detection and correction
, majority logic decoding is a method to decode repetition code
s, based on the assumption that the largest number of occurrences of a symbol was the transmitted symbol.
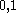 , if a
, if a  repetition code is used, then each input bit is mapped to the code word
repetition code is used, then each input bit is mapped to the code word
as a string of -replicated input bits. Generally
-replicated input bits. Generally 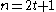 , an odd number.
, an odd number.
The repetition codes can detect up to transmission errors. Decoding errors occur when the more than these transmission errors occur. Thus, assuming bit-transmission errors are independent, the probability of error for a repetition code is given by
transmission errors. Decoding errors occur when the more than these transmission errors occur. Thus, assuming bit-transmission errors are independent, the probability of error for a repetition code is given by 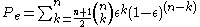 , where
, where  is the error over the transmission channel.
is the error over the transmission channel.
 , where
, where  , an odd number.
, an odd number.
 code, if R=[1 0 1 1 0], then
code, if R=[1 0 1 1 0], then
it would be decoded as,
Error detection and correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
, majority logic decoding is a method to decode repetition code
Repetition code
In coding theory, the repetition code is one of the most basic error-correcting codes. In order to transmit a message over a noisy channel that may corrupt the transmission in a few places, the idea of the repetition code is to just repeat the message several times. The hope is that the channel...
s, based on the assumption that the largest number of occurrences of a symbol was the transmitted symbol.
Theory
In a binary alphabet made of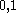 , if a
, if a  repetition code is used, then each input bit is mapped to the code word
repetition code is used, then each input bit is mapped to the code wordCode word
In communication, a code word is an element of a standardized code or protocol. Each code word is assembled in accordance with the specific rules of the code and assigned a unique meaning...
as a string of
 -replicated input bits. Generally
-replicated input bits. Generally 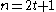 , an odd number.
, an odd number.The repetition codes can detect up to
 transmission errors. Decoding errors occur when the more than these transmission errors occur. Thus, assuming bit-transmission errors are independent, the probability of error for a repetition code is given by
transmission errors. Decoding errors occur when the more than these transmission errors occur. Thus, assuming bit-transmission errors are independent, the probability of error for a repetition code is given by 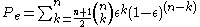 , where
, where  is the error over the transmission channel.
is the error over the transmission channel.Assumptions
The code word is , where
, where  , an odd number.
, an odd number.- Calculate the
 Hamming weightHamming weightThe Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
Hamming weightHamming weightThe Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
of the repetition code. - if
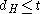 , decode code word to be all 0's
, decode code word to be all 0's - if
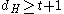 , decode code word to be all 1's
, decode code word to be all 1's
Example
In a code, if R=[1 0 1 1 0], then
code, if R=[1 0 1 1 0], thenit would be decoded as,
-
 ,
, 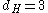 , so R'=[1 1 1 1 1]
, so R'=[1 1 1 1 1] - Hence the transmitted message bit was 1.

