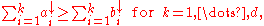Majorization
Encyclopedia
In mathematics
, majorization is a partial order
on vectors
of real numbers. For a vector
, we denote by 
the vector with the same components, but sorted in decreasing order.
Given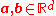
, we say that
weakly majorizes (or dominates) 
written as 
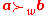iff
where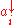
and 
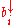are the elements of 
and 
, respectively, sorted in decreasing order.
Equivalently, we say that
is weakly majorized (or dominated) by 
, denoted as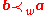 
.
If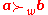
and in addition 
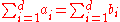we say that
majorizes (or dominates) 
written as 
.
Equivalently, we say that
is majorized (or dominated) by 
, denoted as 
.
Regrettably, to confuse the matter, some literature sources use the reverse notation, e.g.,
is replaced with 
, most notably, in Horn and Johnson, Matrix analysis (Cambridge Univ. Press, 1985), Definition 4.3.24, while the same authors switch to the traditional notation, introduced here, later in their Topics in Matrix Analysis (1994).
A function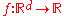
is said to be Schur convex when 
implies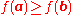 
. Similarly, 
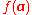is Schur concave when 
implies 
The majorization partial order on finite sets, described here, can be generalized to the Lorenz ordering, a partial order on distribution functions
.
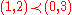is simply
equivalent to
.
(Strong) majorization: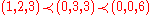
. For vectors with n components
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, majorization is a partial order
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
on vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of real numbers. For a vector
, we denote by the vector with the same components, but sorted in decreasing order.Given
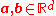, we say that weakly majorizes (or dominates) written as 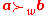iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
where
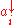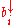and are the elements of and , respectively, sorted in decreasing order.Equivalently, we say that
is weakly majorized (or dominated) by , denoted as 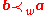.If
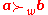and in addition 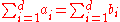we say that majorizes (or dominates) written as .Equivalently, we say that
is majorized (or dominated) by , denoted as .Regrettably, to confuse the matter, some literature sources use the reverse notation, e.g.,
is replaced with , most notably, in Horn and Johnson, Matrix analysis (Cambridge Univ. Press, 1985), Definition 4.3.24, while the same authors switch to the traditional notation, introduced here, later in their Topics in Matrix Analysis (1994).A function
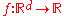is said to be Schur convex when implies 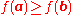. Similarly, 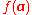is Schur concave when implies The majorization partial order on finite sets, described here, can be generalized to the Lorenz ordering, a partial order on distribution functions
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
.
Examples
The order of the entries does not affect the majorization, e.g., the statement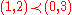 is simplyequivalent to
.(Strong) majorization:
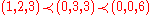. For vectors with n components
-
(Weak) majorization:
. For vectors with n components:
-
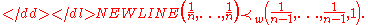
Geometry of Majorization
For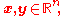
we have
if and only if 
is in the convex hull of all vectors obtained by permuting the coordinates of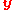 
.
Figure 1 displays the convex hull in 2D for the vector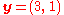
. Notice that the center of the convex hull, which is an interval in this case, is the vector 
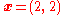. This is the "smallest" vector satisfying 
for this given vector 
.
Figure 2 shows the convex hull in 3D. The center of the convex hull, which is a 2D polygon in this case, is the "smallest" vector
satisfying 
for this given vector 
.
Equivalent conditions
Each of the following statements is true if and only if
:
-
for some doubly stochastic matrixDoubly stochastic matrixIn mathematics, especially in probability and combinatorics, a doubly stochastic matrix,is a square matrix of nonnegative real numbers, each of whose rows and columns sums to 1...
(see Arnold, Theorem 2.1). - From
we can produce 
by a finite sequence of "Robin Hood operations" where we replace two elements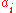 
and 
with 
and 
, respectively, for some 
(see Arnold, p. 11). - For every convex function
, 
(see Arnold, Theorem 2.9).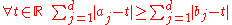 
. (see Nielsen and Chuang Exercise 12.17,)
In linear algebra
- Suppose that for two real vectors
, 
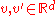majorizes 
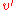. Then it can be shown that there exists a set of probabilities 
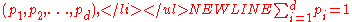and a set of permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s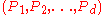
such that 
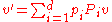. Alternatively it can be shown that there exists a doubly stochastic matrixDoubly stochastic matrixIn mathematics, especially in probability and combinatorics, a doubly stochastic matrix,is a square matrix of nonnegative real numbers, each of whose rows and columns sums to 1...
such that 
- We say that a hermitian operator,
, majorizes another, 
, if the set of eigenvalues of 
majorizes that of 
.
In recursion theory
Given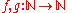
, then 
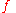is said to majorize 
if, for all 
, 
. If there is some 
so that 
for all 
, then 
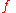is said to dominate (or eventually dominate) 
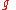. Alternatively, the preceding terms are often defined requiring the strict inequality 
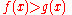instead of 
in the foregoing definitions.
External links
Software
- OCTAVEOctaveIn music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
/MATLABMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
code to check majorization
- We say that a hermitian operator,
-
-