
Manakov system
Encyclopedia
Maxwell's Equations
, when converted to cylindrical coordinates, and with the boundary conditions for an optical fiber
while including birefringence
as an effect taken into account, will yield the coupled nonlinear Schrödinger equation
s. After employing the Inverse scattering transform
(a procedure analogous to the Fourier Transform
and Laplace Transform) on the resulting equations, the Manakov system is then obtained. The most general form of the Manakov system is as follows:

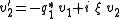
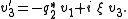
It is a coupled system of linear ordinary differential equations. The functions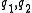 represent the envelope of the electromagnetic field as an initial condition.
represent the envelope of the electromagnetic field as an initial condition.
For theoretical purposes, the integral equation
version is often very useful. It is as follows:
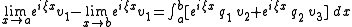
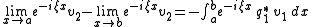

One may make further substitutions and simplifications, depending on the limits used and the assumptions about boundary or initial conditions. One important concept is that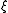 is complex; assumptions must be made about this eigenvalue parameter. If a non-zero solution is desired, the imaginary part of the eigenvalue cannot change sign
is complex; assumptions must be made about this eigenvalue parameter. If a non-zero solution is desired, the imaginary part of the eigenvalue cannot change sign
; accordingly, most researchers take the imaginary part to be positive.
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, when converted to cylindrical coordinates, and with the boundary conditions for an optical fiber
Optical fiber
An optical fiber is a flexible, transparent fiber made of a pure glass not much wider than a human hair. It functions as a waveguide, or "light pipe", to transmit light between the two ends of the fiber. The field of applied science and engineering concerned with the design and application of...
while including birefringence
Birefringence
Birefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
as an effect taken into account, will yield the coupled nonlinear Schrödinger equation
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
s. After employing the Inverse scattering transform
Inverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
(a procedure analogous to the Fourier Transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
and Laplace Transform) on the resulting equations, the Manakov system is then obtained. The most general form of the Manakov system is as follows:

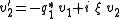
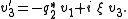
It is a coupled system of linear ordinary differential equations. The functions
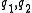 represent the envelope of the electromagnetic field as an initial condition.
represent the envelope of the electromagnetic field as an initial condition.For theoretical purposes, the integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
version is often very useful. It is as follows:
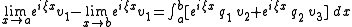
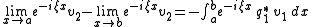

One may make further substitutions and simplifications, depending on the limits used and the assumptions about boundary or initial conditions. One important concept is that
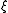 is complex; assumptions must be made about this eigenvalue parameter. If a non-zero solution is desired, the imaginary part of the eigenvalue cannot change sign
is complex; assumptions must be made about this eigenvalue parameter. If a non-zero solution is desired, the imaginary part of the eigenvalue cannot change signSign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
; accordingly, most researchers take the imaginary part to be positive.

