
Margulis lemma
Encyclopedia
In mathematics
, the Margulis lemma (named after Grigory Margulis
) is a result about discrete subgroups of isometries of a symmetric space
(e.g. the hyperbolic n-space
), or more generally a space of non-positive curvature
.
Theorem: Let S be a Riemannian symmetric space
of non-compact type. There is a positive constant

with the following property. Let F be subset of isometries of S. Suppose there is a point x in S such that
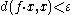
for all f in F. Assume further that the subgroup generated by F is discrete in Isom(S). Then
generated by F is discrete in Isom(S). Then  is virtually nilpotent. More precisely, there exists a subgroup
is virtually nilpotent. More precisely, there exists a subgroup 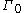 in
in 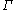 which is nilpotent
which is nilpotent
of nilpotency class at most r and of index
at most N in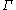 , where r and N are constants depending on S only.
, where r and N are constants depending on S only.
The constant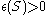 is often referred as the Margulis constant.
is often referred as the Margulis constant.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Margulis lemma (named after Grigory Margulis
Grigory Margulis
Gregori Aleksandrovich Margulis is a Russian mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in Mathematics in 2005, becoming the...
) is a result about discrete subgroups of isometries of a symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
(e.g. the hyperbolic n-space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
), or more generally a space of non-positive curvature
Non-positive curvature
In mathematics, spaces of non-positive curvature occur in many contexts and form a generalization of hyperbolic geometry. In the category of Riemannian manifolds, one can consider the sectional curvature of the manifold and require that this curvature be everywhere less than or equal to zero...
.
Theorem: Let S be a Riemannian symmetric space
Riemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
of non-compact type. There is a positive constant

with the following property. Let F be subset of isometries of S. Suppose there is a point x in S such that
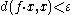
for all f in F. Assume further that the subgroup
 generated by F is discrete in Isom(S). Then
generated by F is discrete in Isom(S). Then  is virtually nilpotent. More precisely, there exists a subgroup
is virtually nilpotent. More precisely, there exists a subgroup 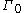 in
in 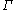 which is nilpotent
which is nilpotentNilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
of nilpotency class at most r and of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
at most N in
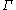 , where r and N are constants depending on S only.
, where r and N are constants depending on S only.The constant
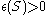 is often referred as the Margulis constant.
is often referred as the Margulis constant.

