In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Markus-Yamabe conjecture is a conjecture

Conjecture

A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...

 on global asymptotic stability

Asymptotic stability

In control theory, a continuous linear time-invariant system is exponentially stable if and only if the system has eigenvalues with strictly negative real parts....

. The conjecture states that if a continuously differentiable

Smooth function

In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...

 map on an -dimensional real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

 has a single fixed point

Fixed point (mathematics)

In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...

, and its Jacobian matrix is everywhere Hurwitz

Hurwitz matrix

-Hurwitz matrix and the Hurwitz stability criterion:In mathematics, Hurwitz matrix is a structured real square matrix constructed with coefficientsof a real polynomial...

, then the fixed point is globally stable.

The conjecture is true for the two-dimensional case. However, counterexamples have been constructed in higher dimensions. Hence, in the two-dimensional case only, it can also be referred to as the Markus-Yamabe theorem.

Related mathematical results concerning global asymptotic stability, which are applicable in dimensions higher than two, include various autonomous convergence theorem

Autonomous convergence theorem

In mathematics, an autonomous convergence theorem is one of a family of related theorems which specify conditions guaranteeing global asymptotic stability of a continuous autonomous dynamical system.-History:...

s. A modified version of the Markus-Yamabe conjecture has been proposed, but at present this new conjecture remains unproven.

Mathematical statement of conjecture

Let 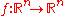be a 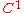map with 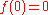and Jacobian 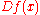which is Hurwitz stable for every .

Then is a global attractor of the dynamical system .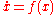

The conjecture is true for and false in general for .