Marriage theorem
Encyclopedia
In mathematics, Hall's marriage theorem is a combinatorial
result that gives the condition allowing the selection of a distinct element from each of a collection of finite sets. It was proved by .
A transversal
for S is a set X and a
bijection
f from X to S such that for all x in X, x is a member of f(x).
An alternative term for transversal is system of distinct representatives
or "SDR".
The collection S satisfies the marriage condition if and only if
for each subcollection
, we have
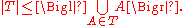
In other words, the number of
subsets in each subcollection T is less than or equal to the number of distinct elements in the
union over the subcollection T.
Hall's theorem states that S has a transversal (SDR) if and only if S satisfies the marriage condition.
A valid SDR would be {1, 4, 5}. (Note this is not unique: {2, 1, 3} works equally well, for example.)
Example 2: Consider S = {S1, S2, S3, S4} with
No valid SDR exists; the marriage condition is violated as is shown by the subcollection {S2, S3, S4}.
The standard example of an application of the marriage theorem is to imagine two groups; one of n men, and one of n women. For each woman, there is a subset of the men any one of which she would happily marry; and any man would be happy to marry a woman who wants to marry him. Consider whether it is possible to pair up (in marriage
) the men and women so that every person is happy.
If we let Si be the set of men that the i-th woman would be happy to marry, then the marriage theorem states that each woman can happily marry a man if and only if the collection of sets {Si} meets the marriage condition.
Note that the marriage condition is that, for any subset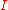
of the women, the number of men whom at least one of the women would be happy to marry, 
, be at least as big as the number of women in that subset,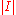 
. It is obvious that this condition is necessary, as if it does not hold, there are not enough men to share among the 
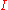women. What is interesting is that it is also a sufficient condition.
The theorem has many other interesting "non-marital" applications. For example, take a standard deck of cards
, and deal them out into 13 piles of 4 cards each. Then, using the marriage theorem, we can show that it is always possible to select exactly 1 card from each pile, such that the 13 selected cards contain exactly one card of each rank (ace, 2, 3, ..., queen, king).
More abstractly, let G be a group
, and H be a finite subgroup
of G. Then the marriage theorem can be used to show that there is a set X such that X is an SDR for both the set of left coset
s and right cosets of H in G.
The more general problem of selecting a (not necessarily distinct) element from each of a collection of sets is permitted in general only if the axiom of choice is accepted.
Suppose G(X,Y) is a bipartite graph and M is a matching which saturates every vertex of X.
Consider the set of all vertices in Y which saturates a given S by the matching M to be M(S). Therefore, |M(S)|=|S|, by definition of matching.
But M(S) C N(S), since all elements of M(S) are neighbours of S.
So, |N(S)| ≥ |M(S)| and hence, |N(S)| ≥ |S|.
Now we prove: If |N(S)| ≥ |S| for all S C X, then G(X,Y) has a matching which saturates every vertex in X.
Assume G(X,Y) is a bipartite graph that has no matching M which saturates all vertices of X.
Consider a set S containing vertex u which is not saturated by a maximum matching M. Consider all augmenting paths starting from u.
Let the set of all points in Y connected to u by these augmenting paths be T.
Consider set of all vertices of S (in X) in these paths such that S \ u is saturated by M. So, |M(S)|=|S|-1, as u is not in a matching.
But, all vertices in T are connected to u and set of all vertices connected to a vertex in S\u is in T. Therefore, |N(S)|=|T|.
But |N(u)|=|T| as all neighbours of u are included in T. Also, for every vertex connected to u in T there exists a corresponding matching to another vertex in S.
Hence, |N(u)|=number of matchings=|M(S)|=|S|-1.
But |N(u)|=|T|=|N(S)|.
Thus, |N(S)|=|S|-1 which implies |N(S)|<|S| (contradiction).
Hence our assumption that G has no matching is false, therefore, G has a matching.
. Formulated in graph theoretic terms the problem can be stated as:
Given a finite bipartite graph
G:= (S + T, E) with two equally sized partitions S and T, does there exist a perfect matching, i.e. a set of edges so that every vertex of G is incident to precisely one of them?
The marriage theorem provides the answer:
For a set X of vertices of G, let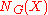
denote the neighborhood
of X in G, i.e. the set of all vertices adjacent
to some element of X. The Marriage theorem (Hall's Theorem) for Graph theory states that a perfect matching exists if and only if
for every subset X of S
In other words every subset X of S has enough adjacent vertices in T.
A generalization to arbitrary graphs is provided by Tutte theorem
.
for all subsets X of S.
In particular, there are simple proofs of the implications Dilworth's theorem ⇒ Hall's theorem ⇔ König–Egerváry theorem ⇔ König's theorem.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
result that gives the condition allowing the selection of a distinct element from each of a collection of finite sets. It was proved by .
Definitions and statement of the theorem
Let S be a collection of finite sets.A transversal
Transversal
In geometry , when two coplanar lines exist such that a third coplanar line passes thru both lines. This third line is named the Transversal....
for S is a set X and a
bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
f from X to S such that for all x in X, x is a member of f(x).
An alternative term for transversal is system of distinct representatives
or "SDR".
The collection S satisfies the marriage condition if and only if
for each subcollection
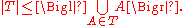
, we haveIn other words, the number of
subsets in each subcollection T is less than or equal to the number of distinct elements in the
union over the subcollection T.
Hall's theorem states that S has a transversal (SDR) if and only if S satisfies the marriage condition.
Discussion and examples
Example 1: Consider S = {S1, S2, S3} with- S1 = {1, 2, 3}
- S2 = {1, 4, 5}
- S3 = {3, 5}.
A valid SDR would be {1, 4, 5}. (Note this is not unique: {2, 1, 3} works equally well, for example.)
Example 2: Consider S = {S1, S2, S3, S4} with
- S1 = {2, 3, 4, 5}
- S2 = {4, 5}
- S3 = {5}
- S4 = {4}.
No valid SDR exists; the marriage condition is violated as is shown by the subcollection {S2, S3, S4}.
The standard example of an application of the marriage theorem is to imagine two groups; one of n men, and one of n women. For each woman, there is a subset of the men any one of which she would happily marry; and any man would be happy to marry a woman who wants to marry him. Consider whether it is possible to pair up (in marriage
Marriage
Marriage is a social union or legal contract between people that creates kinship. It is an institution in which interpersonal relationships, usually intimate and sexual, are acknowledged in a variety of ways, depending on the culture or subculture in which it is found...
) the men and women so that every person is happy.
If we let Si be the set of men that the i-th woman would be happy to marry, then the marriage theorem states that each woman can happily marry a man if and only if the collection of sets {Si} meets the marriage condition.
Note that the marriage condition is that, for any subset
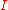of the women, the number of men whom at least one of the women would be happy to marry, , be at least as big as the number of women in that subset, 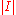. It is obvious that this condition is necessary, as if it does not hold, there are not enough men to share among the 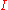women. What is interesting is that it is also a sufficient condition.The theorem has many other interesting "non-marital" applications. For example, take a standard deck of cards
Playing card
A playing card is a piece of specially prepared heavy paper, thin cardboard, plastic-coated paper, cotton-paper blend, or thin plastic, marked with distinguishing motifs and used as one of a set for playing card games...
, and deal them out into 13 piles of 4 cards each. Then, using the marriage theorem, we can show that it is always possible to select exactly 1 card from each pile, such that the 13 selected cards contain exactly one card of each rank (ace, 2, 3, ..., queen, king).
More abstractly, let G be a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, and H be a finite subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G. Then the marriage theorem can be used to show that there is a set X such that X is an SDR for both the set of left coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s and right cosets of H in G.
The more general problem of selecting a (not necessarily distinct) element from each of a collection of sets is permitted in general only if the axiom of choice is accepted.
Proof
We first prove: If G has a matching which covers every vertex in X then |N(S)| ≥ |S| for all S C X.Suppose G(X,Y) is a bipartite graph and M is a matching which saturates every vertex of X.
Consider the set of all vertices in Y which saturates a given S by the matching M to be M(S). Therefore, |M(S)|=|S|, by definition of matching.
But M(S) C N(S), since all elements of M(S) are neighbours of S.
So, |N(S)| ≥ |M(S)| and hence, |N(S)| ≥ |S|.
Now we prove: If |N(S)| ≥ |S| for all S C X, then G(X,Y) has a matching which saturates every vertex in X.
Assume G(X,Y) is a bipartite graph that has no matching M which saturates all vertices of X.
Consider a set S containing vertex u which is not saturated by a maximum matching M. Consider all augmenting paths starting from u.
Let the set of all points in Y connected to u by these augmenting paths be T.
Consider set of all vertices of S (in X) in these paths such that S \ u is saturated by M. So, |M(S)|=|S|-1, as u is not in a matching.
But, all vertices in T are connected to u and set of all vertices connected to a vertex in S\u is in T. Therefore, |N(S)|=|T|.
But |N(u)|=|T| as all neighbours of u are included in T. Also, for every vertex connected to u in T there exists a corresponding matching to another vertex in S.
Hence, |N(u)|=number of matchings=|M(S)|=|S|-1.
But |N(u)|=|T|=|N(S)|.
Thus, |N(S)|=|S|-1 which implies |N(S)|<|S| (contradiction).
Hence our assumption that G has no matching is false, therefore, G has a matching.
Graph theory
The marriage theorem has applications in the area of graph theoryGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. Formulated in graph theoretic terms the problem can be stated as:
Given a finite bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
G:= (S + T, E) with two equally sized partitions S and T, does there exist a perfect matching, i.e. a set of edges so that every vertex of G is incident to precisely one of them?
The marriage theorem provides the answer:
For a set X of vertices of G, let
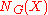denote the neighborhoodNeighbourhood (graph theory)
In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the induced subgraph of G consisting of all vertices adjacent to v and all edges connecting two such vertices. For example, the image shows a...
of X in G, i.e. the set of all vertices adjacent
Adjacent
Adjacent is an adjective meaning contiguous, adjoining or abuttingIn geometry, adjacent is when sides meet to make an angle.In graph theory adjacent nodes in a graph are linked by an edge....
to some element of X. The Marriage theorem (Hall's Theorem) for Graph theory states that a perfect matching exists if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for every subset X of S
In other words every subset X of S has enough adjacent vertices in T.
A generalization to arbitrary graphs is provided by Tutte theorem
Tutte theorem
In the mathematical discipline of graph theory the Tutte theorem, named after William Thomas Tutte, is a characterization of graphs with perfect matchings...
.
A more general statement
Let G:= (S + T, E) be a finite bipartite graph with S and T not necessarily equally sized. Then G contains a matching of S into T if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for all subsets X of S.
Logical equivalences
This theorem is part of a collection of remarkably powerful theorems in combinatorics, all of which are related to each other in an informal sense in that it is more straightforward to prove one of these theorems from another of them than from first principles. These include:- The König–Egerváry theorem (1931) (Dénes KőnigDénes KönigDénes Kőnig was a Jewish Hungarian mathematician who worked in and wrote the first textbook on the field of graph theory....
, Jenő EgerváryJenő EgerváryJenő Egerváry was a Hungarian mathematician.-Biography:Egerváry was born in Debrecen in 1891. In 1914, he received his doctorate at the Pázmány Péter University in Budapest, where he studied under the supervision of Lipót Fejér...
) - Menger's theoremMenger's theoremIn the mathematical discipline of graph theory and related areas, Menger's theorem is a basic result about connectivity in finite undirected graphs. It was proved for edge-connectivity and vertex-connectivity by Karl Menger in 1927...
(1927) - The max-flow min-cut theoremMax-flow min-cut theoremIn optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the minimum capacity which when removed in a specific way from the network causes the situation that no flow can pass from the source to the...
(Ford–Fulkerson algorithm) - The Birkhoff–Von Neumann theorem (1946)
- Dilworth's theoremDilworth's theoremIn mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains...
.
In particular, there are simple proofs of the implications Dilworth's theorem ⇒ Hall's theorem ⇔ König–Egerváry theorem ⇔ König's theorem.
External links
- Marriage Theorem at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Marriage Theorem and Algorithm at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...