Martin's maximum
Encyclopedia
In set theory
, Martin's maximum, introduced by , is a generalization of the proper forcing axiom
, which is in turn a generalization of Martin's axiom
.
Martin's maximum (MM) states that if D is a collection of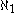
dense subsets of a notion of forcing that preserves stationary subsets of ω1, then there is a D-generic filter. It is a well known fact that forcing with a ccc notion of forcing preserves stationary subsets of ω1, thus MM extends MA(
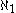). If (P,≤) is not a stationary set preserving notion of forcing, i.e., there is a stationary subset of ω1, which becomes nonstationary when forcing with (P,≤), then there is a collection D of 
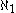dense subsets of (P,≤), such that there is no D-generic filter. This is why MM is called the maximal extension of Martin's axiom.
The existence of a supercompact cardinal implies the consistency of Martin's maximum. The proof uses Shelah
's theories of semiproper forcing and iteration with revised countable supports.
MM implies that the value of the continuum
is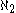
and that the ideal of nonstationary sets
on ω1 is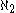
-saturated. It further implies stationary reflection, i.e., if S is a stationary subset of some regular cardinal κ≥ω2 and every element of S has countable cofinality, then there is an ordinal α<κ such that S∩α is stationary in α. In fact, S contains a closed subset of order type ω1.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, Martin's maximum, introduced by , is a generalization of the proper forcing axiom
Proper Forcing Axiom
In the mathematical field of set theory, the proper forcing axiom is a significant strengthening of Martin's axiom, where forcings with the countable chain condition are replaced by proper forcings.- Statement :...
, which is in turn a generalization of Martin's axiom
Martin's axiom
In the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
.
Martin's maximum (MM) states that if D is a collection of
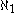dense subsets of a notion of forcing that preserves stationary subsets of ω1, then there is a D-generic filter. It is a well known fact that forcing with a ccc notion of forcing preserves stationary subsets of ω1, thus MM extends MA(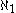). If (P,≤) is not a stationary set preserving notion of forcing, i.e., there is a stationary subset of ω1, which becomes nonstationary when forcing with (P,≤), then there is a collection D of 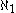dense subsets of (P,≤), such that there is no D-generic filter. This is why MM is called the maximal extension of Martin's axiom.The existence of a supercompact cardinal implies the consistency of Martin's maximum. The proof uses Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
's theories of semiproper forcing and iteration with revised countable supports.
MM implies that the value of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
is
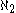and that the ideal of nonstationary setsStationary set
In mathematics, particularly in set theory and model theory, there are at least three notions of stationary set:-Classical notion:If \kappa \, is a cardinal of uncountable cofinality, S \subseteq \kappa \,, and S \, intersects every club set in \kappa \,, then S \, is called a stationary set....
on ω1 is
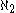-saturated. It further implies stationary reflection, i.e., if S is a stationary subset of some regular cardinal κ≥ω2 and every element of S has countable cofinality, then there is an ordinal α<κ such that S∩α is stationary in α. In fact, S contains a closed subset of order type ω1.