Mathematics of bookmaking
Encyclopedia
In betting parlance, making a book is the practice of laying bets on the various possible outcomes of a single event. The term originates from the practice of recording such wagers in a hard-bound ledger (the 'book') and gives the English language the term bookmaker
for the person laying the bets and thus 'making the book'.
and coherence (philosophical gambling strategy)
. This is achieved primarily by adjusting what are determined to be the true odds
of the various outcomes of an event in a downward fashion (i.e. the bookmaker will pay out using his actual odds, an amount which is less than the true odds would have paid; thus hopefully ensuring a profit).
The odds quoted for a particular event may be fixed (as in the case of a football match for example) or may fluctuate to take account of the size of wagers placed by the bettors in the run-up to the actual event (e.g. a horse race). This article explains the mathematics of making a book in the (simpler) case of the former event. For the second method, see Parimutuel betting
It is important to understand the relationship between odds and relative probabilities:
Thus, odds of a-b (a/b or a to b) represent a relative probability of b/(a + b), e.g. 6-4 (6 to 4) is 4/(6 + 4) = 4/10 = 0.4 (or 40%).
A relative probability of x represents odds of (1 − x)/x, e.g. 0.2 is (1 − 0.2)/0.2 = 0.8/0.2 = 4/1 (4-1, 4 to 1).
These odds can be represented as relative probabilities (or percentages by multiplying by 100) as follows:
By adding the percentages together a total 'book' of 100% is achieved (representing a fair book). The bookmaker, in his wish to avail himself of a profit, will invariably reduce these odds - possibly to the following:
By adding these percentages together a 'book' of 111%, or approximately 111.27%, is achieved.
The amount by which the actual 'book' exceeds 100% is known as the 'overround': it represents the bookmaker's potential profit if he is fortunate enough to accept bets in the exact proportions required. Thus, in an ideal situation, if the bookmaker accepts £111.27 in bets at his own quoted odds in the correct proportion, he will pay out only £100 (including returned stakes) no matter what the actual outcome of the football match.
Examining how he potentially achieves this:
Total stakes received — £111.27 and a maximum payout of £100 irrespective of the result. This £11.27 profit represents a 10.1% profit on turnover (11.27 × 100/111.27).
To explain the concept in the most basic of situations an example consisting of a double made up of selecting the winner from each of two tennis matches will be looked at:
In Match 1 between players A and B both players are assessed to have an equal chance of winning. The situation is the same in Match 2 between players C and D. In a fair book in each of their matches, i.e. each has a book of 100%, all players would be offered at odds of Evens. However, a bookmaker would probably offer odds of 5-6 (for example) on each of the two possible outcomes in each event (each tennis match). This results in a book for each of the tennis matches of 109.09...%, calculated by 100 × ( + ) i.e. 9.09% overround.
There are four possible outcomes from combining the results from both matches: the winning pair of players could be AC, AD, BC or BD. As each of the outcomes for this example has been deliberately chosen to ensure that they are equally likely it can be deduced that the probability of each outcome occurring is or 0.25 and that the odds against each one occurring is 3-1 (3/1 or 'three to one'). A bet of 100 units (for simplicity) on any of the winning combinations would produce a return of 100 × (3/1 + 1) = 400 units.
As detailed below, the actual return on any of these winning doubles is obtained by multiplying stake × ('odds plus one' from each single bet) together. Thus for a stake of 100 units we get a return of 100 × (5/6 + 1) × (5/6 + 1) = 336.11... units, representing odds of 2.3611-1 which is far less than the true 3-1.
Odds of 2.3611-1 represent a percentage of 29.752% (100/3.3611) and multiplying by 4 for the total number of equally likely outcomes gives a total book of 119.01%. Thus the overround has slightly more than doubled by combining two single bets into a double.
In general, the combined overround on a double (OD), expressed as a percentage, is calculated from the individual books B1 and B2, expressed as decimals, by OD = B1 × B2 × 100 − 100.
In the example we have OD = 1.0909 × 1.0909 × 100 − 100 = 19.01%.
This massive increase in potential profit for the bookmaker (19% instead of 9% on an event; in this case the double) is the main reason why bookmakers pay bonuses for the successful selection of winners in multiple bets: compare offering a 25% bonus on the correct choice of four winners from four selections in a Yankee, for example, when the potential overround on a simple fourfold of races with individual books of 120% is over 107% (a book of 207%). This is why bookmakers offer bets such as Lucky 15, Lucky 31 and Lucky 63; offering double the odds for one winner and increasing percentage bonuses for two, three and more winners.
In general, for any accumulator bet from two to i selections, the combined percentage overround of books of B1, B2, ..., Bi given in terms of decimals, is calculated by B1 × B2 × ... × Bi × 100 − 100. E.g. the previously mentioned fourfold consisting of individual books of 120% (1.20) gives an overround of 1.20 × 1.20 × 1.20 × 1.20 × 100 − 100 = 107.36%.
E.g. £100 single at 9-2; total staked = £100
Each-way single
E.g. £100 each-way single at 11-4 ( odds a place); total staked = £200
Double
E.g. £100 each-way double with winners at 2-1 ( odds a place) and 5-4 ( odds a place); total staked = £200
Note: "Win to Win, Place to Place" will always provide a greater return if all selections win, whereas "Each-Way all Each-Way" provides greater compensation if one selection is a loser as each of the other winners provide a greater amount of place money for subsequent selections.
Treble
E.g. £100 treble with winners at 3-1, 4-6 and 11-4; total staked = £100
Accumulator
E.g. £100 each-way fivefold accumulator with winners at Evens ( odds a place), 11-8 ( odds), 5-4 ( odds), 1-2 (all up to win) and 3-1 ( odds); total staked = £200
Note: 'All up to win' means there are insufficient participants in the event for place odds to be given (e.g. 4 or fewer runners in a horse race). The only 'place' therefore is first place, for which the win odds are given.
Yankee
Trixie, Yankee, Canadian, Heinz, Super Heinz and Goliath form a family of bets known as full cover bet
s which have all possible multiples present. Examples of winning Trixie and Yankee bets have been shown above. The other named bets are calculated in a similar way by looking at all the possible combinations of selections in their multiples. Note: A Double may be thought of as a full cover bet with only two selections.
Should a selection in one of these bets not win, then the remaining winners are treated as being a wholly successful bet on the next 'family member' down. For example, only two winners out of three in a Trixie means the bet is settled as a double; only four winners out of five in a Canadian means it is settled as a Yankee; only five winners out of eight in a Goliath means it is settled as a Canadian. The place part of each-way bets is calculated separately using reduced place odds. Thus, an each-way Super Heinz on seven horses with three winners and a further two placed horses is settled as a win Trixie and a place Canadian. Virtually all bookmakers use computer software for ease, speed and accuracy of calculation for the settling of multiples bets.
Patent, Lucky 15, Lucky 31, Lucky 63 and higher Lucky bets form a family of bets known as full cover bets with singles
which have all possible multiples present together with single bets on all selections. An examples of a winning Patent bet has been shown above. The other named bets are calculated in a similar way by looking at all the possible combinations of selections in their multiples and singles.
Should a selection in one of these bets not win, then the remaining winners are treated as being a wholly successful bet on the next 'family member' down. For example, only two winners out of three in a Patent means the bet is settled as a double and two singles; only three winners out of four in a Lucky 15 means it is settled as a Patent; only four winners out of six in a Lucky 63 means it is settled as a Lucky 15. The place part of each-way bets is calculated separately using reduced place odds. Thus, an each-way Lucky 63 on six horses with three winners and a further two placed horses is settled as a win Patent and a place Lucky 31.
If a, b, c, d... represent the decimal odds, i.e. (fractional odds + 1), then an OM can be calculated algebraically by multiplying the expressions (a + 1), (b + 1), (c + 1)... etc. together in the required manner and subtracting 1. If required, (decimal odds + 1) may be replaced by (fractional odds + 2).
Expanding (a + 1)(b + 1)(c + 1) algebraically gives abc + ab + ac + bc + a + b + c + 1. This is equivalent to the OM for a Patent (treble: abc; doubles: ab, ac and bc; singles: a, b and c) plus 1.
Therefore to calculate the returns for a winning Patent it is just a case of multiplying (a + 1), (b + 1) and (c + 1) together and subtracting 1 to get the OM for the winning bet, i.e. OM = (a + 1)(b + 1)(c + 1) − 1. Now multiply by the unit stake to get the total return on the bet.
E.g. The winning Patent described earlier can be more quickly and simply evaluated by the following:
Ignoring any bonuses, a 50 pence each-way Lucky 63 (total stake £63) with 4 winners [2-1, 5-2, 7-2 (all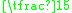
odds a place) and 6-4 ( 
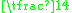odds a place)] and a further placed horse [9-2 ( 
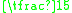odds a place)] can be relatively easily calculated as follows:
For the family of full cover bets that do not include singles an adjustment to the calculation is made to leave just the doubles, trebles and accumulators. Thus, a previously described winning £10 Yankee with winners at 1-3, 5-2, 6-4 and Evens has returns calculated by:
In effect, the bet has been calculated as a Lucky 15 minus the singles. Note that the total returns value of £999.16 is a penny higher than the previously calculated value as this quicker method only involves rounding the final answer, and not rounding at each individual step.
In algebraic terms the OM for the Yankee bet is given by:
In the days before software became available for use by bookmakers and those settling bets in Licensed Betting Offices (LBOs) this method was virtually de rigueur for saving time and avoiding the multiple repetitious calculations necessary in settling bets of the full cover type.
Round Robin
A Round Robin with 3 winners is calculated as a Trixie plus three Up and Down bets with 2 winners in each.
A Round Robin with 2 winners is calculated as a double plus one Up and Down bet with 2 winners plus two Up and Down bets with 1 winner in each.
A Round Robin with 1 winner is calculated two Up and Down bets with one winner in each.
Flag and Super Flag bets may be calculated in a similar manner as above using the appropriate full cover bet (if sufficient winners) together with the required number of 2 winner- and 1 winner Up and Down bets.
Note: Expert bet settlers before the introduction of bet-settling software would have invariably used an algebraic-type method together with a simple calculator to determine the return on a bet (see below).
Bookmaker
A bookmaker, or bookie, is an organization or a person that takes bets on sporting and other events at agreed upon odds.- Range of events :...
for the person laying the bets and thus 'making the book'.
Making a 'book' (and the notion of overround)
A bookmaker strives to accept bets on the outcome of an event in the right proportions so that he makes a profit regardless of which outcome prevails. See Dutch bookDutch book
In gambling a Dutch book or lock is a set of odds and bets which guarantees a profit, regardless of the outcome of the gamble. It is associated with probabilities implied by the odds not being coherent....
and coherence (philosophical gambling strategy)
Coherence (philosophical gambling strategy)
In a thought experiment proposed by the Italian probabilist Bruno de Finetti in order to justify Bayesian probability, an array of wagers is coherent precisely if it does not expose the wagerer to certain loss regardless of the outcomes of events on which he is wagering, even if his opponent makes...
. This is achieved primarily by adjusting what are determined to be the true odds
Odds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
of the various outcomes of an event in a downward fashion (i.e. the bookmaker will pay out using his actual odds, an amount which is less than the true odds would have paid; thus hopefully ensuring a profit).
The odds quoted for a particular event may be fixed (as in the case of a football match for example) or may fluctuate to take account of the size of wagers placed by the bettors in the run-up to the actual event (e.g. a horse race). This article explains the mathematics of making a book in the (simpler) case of the former event. For the second method, see Parimutuel betting
Parimutuel betting
Parimutuel betting is a betting system in which all bets of a particular type are placed together in a pool; taxes and the "house-take" or "vig" is removed, and payoff odds are calculated by sharing the pool among all winning bets...
It is important to understand the relationship between odds and relative probabilities:
Thus, odds of a-b (a/b or a to b) represent a relative probability of b/(a + b), e.g. 6-4 (6 to 4) is 4/(6 + 4) = 4/10 = 0.4 (or 40%).
A relative probability of x represents odds of (1 − x)/x, e.g. 0.2 is (1 − 0.2)/0.2 = 0.8/0.2 = 4/1 (4-1, 4 to 1).
Example
In considering a soccer match (the event) that can be either a 'home win', 'draw' or 'away win' (the outcomes) then the following odds might be encountered to represent the true chance of each of the three outcomes:- Home: Evens
- Draw: 2-1
- Away: 5-1
These odds can be represented as relative probabilities (or percentages by multiplying by 100) as follows:
- Evens (or 1-1) corresponds to a relative probability of (50%)
- 2-1 corresponds to a relative probability of (33%)
- 5-1 corresponds to a relative probability of (16%)
By adding the percentages together a total 'book' of 100% is achieved (representing a fair book). The bookmaker, in his wish to avail himself of a profit, will invariably reduce these odds - possibly to the following:
- Home: 4-5
- Draw: 9-5
- Away: 4-1
- 4-5 corresponds to a relative probability of (55%)
- 9-5 corresponds to a relative probability of (35%)
- 4-1 corresponds to a relative probability of (20%)
By adding these percentages together a 'book' of 111%, or approximately 111.27%, is achieved.
The amount by which the actual 'book' exceeds 100% is known as the 'overround': it represents the bookmaker's potential profit if he is fortunate enough to accept bets in the exact proportions required. Thus, in an ideal situation, if the bookmaker accepts £111.27 in bets at his own quoted odds in the correct proportion, he will pay out only £100 (including returned stakes) no matter what the actual outcome of the football match.
Examining how he potentially achieves this:
- A stake of £55.56 @ 4-5 returns £100.00 (rounded down to nearest penny) for a home win.
- A stake of £35.71 @ 9-5 returns £ 99.98 (rounded down to nearest penny) for a drawn match
- A stake of £20.00 @ 4-1 returns £100.00 (exactly) for an away win
Total stakes received — £111.27 and a maximum payout of £100 irrespective of the result. This £11.27 profit represents a 10.1% profit on turnover (11.27 × 100/111.27).
Overround on multiple bets
When a punter (bettor) combines more than one selection in, for example, a double, treble or accumulator then the effect of the overround in the book of each selection is compounded to the detriment of the punter in terms of the financial return compared to the true odds of all of the selections winning and thus resulting in a successful bet.To explain the concept in the most basic of situations an example consisting of a double made up of selecting the winner from each of two tennis matches will be looked at:
In Match 1 between players A and B both players are assessed to have an equal chance of winning. The situation is the same in Match 2 between players C and D. In a fair book in each of their matches, i.e. each has a book of 100%, all players would be offered at odds of Evens. However, a bookmaker would probably offer odds of 5-6 (for example) on each of the two possible outcomes in each event (each tennis match). This results in a book for each of the tennis matches of 109.09...%, calculated by 100 × ( + ) i.e. 9.09% overround.
There are four possible outcomes from combining the results from both matches: the winning pair of players could be AC, AD, BC or BD. As each of the outcomes for this example has been deliberately chosen to ensure that they are equally likely it can be deduced that the probability of each outcome occurring is or 0.25 and that the odds against each one occurring is 3-1 (3/1 or 'three to one'). A bet of 100 units (for simplicity) on any of the winning combinations would produce a return of 100 × (3/1 + 1) = 400 units.
As detailed below, the actual return on any of these winning doubles is obtained by multiplying stake × ('odds plus one' from each single bet) together. Thus for a stake of 100 units we get a return of 100 × (5/6 + 1) × (5/6 + 1) = 336.11... units, representing odds of 2.3611-1 which is far less than the true 3-1.
Odds of 2.3611-1 represent a percentage of 29.752% (100/3.3611) and multiplying by 4 for the total number of equally likely outcomes gives a total book of 119.01%. Thus the overround has slightly more than doubled by combining two single bets into a double.
In general, the combined overround on a double (OD), expressed as a percentage, is calculated from the individual books B1 and B2, expressed as decimals, by OD = B1 × B2 × 100 − 100.
In the example we have OD = 1.0909 × 1.0909 × 100 − 100 = 19.01%.
This massive increase in potential profit for the bookmaker (19% instead of 9% on an event; in this case the double) is the main reason why bookmakers pay bonuses for the successful selection of winners in multiple bets: compare offering a 25% bonus on the correct choice of four winners from four selections in a Yankee, for example, when the potential overround on a simple fourfold of races with individual books of 120% is over 107% (a book of 207%). This is why bookmakers offer bets such as Lucky 15, Lucky 31 and Lucky 63; offering double the odds for one winner and increasing percentage bonuses for two, three and more winners.
In general, for any accumulator bet from two to i selections, the combined percentage overround of books of B1, B2, ..., Bi given in terms of decimals, is calculated by B1 × B2 × ... × Bi × 100 − 100. E.g. the previously mentioned fourfold consisting of individual books of 120% (1.20) gives an overround of 1.20 × 1.20 × 1.20 × 1.20 × 100 − 100 = 107.36%.
Settling winning bets
In settling winning bets either decimal odds are used or one is added to the fractional odds: this is to include the stake in the return. The place part of each-way bets is calculated separately from the win part; the method is identical but the odds are reduced by whatever the place factor is for the particular event (see Accumulator below for detailed example). All bets are taken as 'win' bets unless 'each-way' is specifically stated. All show use of fractional odds: replace (fractional odds + 1) by decimal odds if decimal odds known. Non-runners are treated as winners with fractional odds of zero (decimal odds of 1). Fractions of pence in total winnings are invariably rounded down by bookmakers to the nearest penny below. Calculations below for multiple-bet wagers result in totals being shown for the separate categories (e.g. doubles, trebles etc.), and therefore overall returns may not be exactly the same as the amount received from using the computer software available to bookmakers to calculate total winnings.Singles
Win singleE.g. £100 single at 9-2; total staked = £100
- Returns = £100 × (9/2 + 1) = £100 × 5.5 = £550
Each-way single
E.g. £100 each-way single at 11-4 ( odds a place); total staked = £200
- Returns (win) = £100 × (11/4 + 1) = £100 × 3.75 = £375
- Returns (place) = £100 × (11/20 + 1) = £100 × 1.55 = £155
- Total returns if selection wins = £530; if only placed = £155
Multiple bets
Each-Way multiple bets are usually settled using a default "Win to Win, Place to Place" method, meaning that the bet consists of a win accumulator and a separate place accumulator (Note: a double or treble is an accumulator with 2 or 3 selections respectively). However, a more uncommon way of settling these type of bets is "Each-Way all Each-Way" (which must normally be requested as such on the betting slip) in which the returns from one selection in the accumulator are split to form an equal-stake each-way bet on the next selection and so on until all selections have been used. The first example below shows the two different approaches to settling these types of bets.Double
E.g. £100 each-way double with winners at 2-1 ( odds a place) and 5-4 ( odds a place); total staked = £200
- Returns (win double) = £100 × (2/1 + 1) × (5/4 + 1) = £675
- Returns (place double) = £100 × (2/5 + 1) × (5/16 + 1) = £183.75
- Total returns = £858.75
- Returns (first selection) = £100 × (2/1 + 1) + £100 × (2/5 + 1) = £440 which is split equally to give a £220 each-way bet on the second selection)
- Returns (second selection) = £220 × (5/4 + 1) + £220 × (5/16 + 1) = £783.75
- Total returns = £783.85
Note: "Win to Win, Place to Place" will always provide a greater return if all selections win, whereas "Each-Way all Each-Way" provides greater compensation if one selection is a loser as each of the other winners provide a greater amount of place money for subsequent selections.
Treble
E.g. £100 treble with winners at 3-1, 4-6 and 11-4; total staked = £100
- Returns = £100 × (3/1 + 1) × (4/6 + 1) × (11/4 + 1) = £2500
Accumulator
E.g. £100 each-way fivefold accumulator with winners at Evens ( odds a place), 11-8 ( odds), 5-4 ( odds), 1-2 (all up to win) and 3-1 ( odds); total staked = £200
Note: 'All up to win' means there are insufficient participants in the event for place odds to be given (e.g. 4 or fewer runners in a horse race). The only 'place' therefore is first place, for which the win odds are given.
- Returns (win fivefold) = £100 × (1/1 + 1) × (11/8 + 1) × (5/4 + 1) × (1/2 + 1) × (3/1 + 1) = £641.25
- Returns (place fivefold) = £100 × (1/4 + 1) × (11/40 + 1) × (5/16 + 1) × (1/2 + 1) × (3/5 + 1) = £502.03
- Total returns = £1143.28
Full-cover bets
Trixie- Returns (3 doubles) = £10 × [(4/7 + 1) × (2/1 + 1) + (4/7 + 1) × (11/10 + 1) + (2/1 + 1) × (11/10 + 1)] = £143.14
- Returns (1 treble) = £10 × (4/7 + 1) × (2/1 + 1) × (11/10 + 1) = £99.00
- Total returns = £242.14
Yankee
- Returns (6 doubles) = £10 × [(1/3 + 1) × (5/2 + 1) + (1/3 + 1) × (6/4 + 1) + (1/3 + 1) × (1/1 + 1) + (5/2 + 1) × (6/4 + 1) + (5/2 + 1) × (1/1 + 1) + (6/4 + 1) × (1/1 + 1)] = £314.16
- Returns (4 trebles) = £10 × [(1/3 + 1) × (5/2 + 1) × (6/4 + 1) + (1/3 + 1) × (5/2 + 1) × (1/1 + 1) + (1/3 + 1) × (6/4 + 1) × (1/1 + 1) + (5/2 + 1) × (6/4 + 1) × (1/1 + 1)] = £451.66
- Returns (1 fourfold) = £10 × (1/3 + 1) × (5/2 + 1) × (6/4 + 1) × (1/1 + 1) = £233.33
- Total returns = £999.15
Trixie, Yankee, Canadian, Heinz, Super Heinz and Goliath form a family of bets known as full cover bet
Full cover bet
A full cover bet is any bet which consists of all available multiple bets over a given number of selections.Examples of full cover bets:* Trixie - three selections* Yankee - four selections* Canadian or Super Yankee - five selections...
s which have all possible multiples present. Examples of winning Trixie and Yankee bets have been shown above. The other named bets are calculated in a similar way by looking at all the possible combinations of selections in their multiples. Note: A Double may be thought of as a full cover bet with only two selections.
Should a selection in one of these bets not win, then the remaining winners are treated as being a wholly successful bet on the next 'family member' down. For example, only two winners out of three in a Trixie means the bet is settled as a double; only four winners out of five in a Canadian means it is settled as a Yankee; only five winners out of eight in a Goliath means it is settled as a Canadian. The place part of each-way bets is calculated separately using reduced place odds. Thus, an each-way Super Heinz on seven horses with three winners and a further two placed horses is settled as a win Trixie and a place Canadian. Virtually all bookmakers use computer software for ease, speed and accuracy of calculation for the settling of multiples bets.
Full cover bets with singles
Patent- Returns (3 singles) = £2 × [(4/6 + 1) + (2/1 + 1) + (11/4 + 1)] = £16.83
- Returns (3 doubles) = £2 × [(4/6 + 1) × (2/1 + 1) + (4/6 + 1) × (11/4 + 1) + (2/1 + 1) × (11/4 + 1)] = £45.00
- Returns (1 treble) = £2 × (4/6 + 1) × (2/1 + 1) × (11/4 + 1) = £37.50
- Total returns = £99.33
Patent, Lucky 15, Lucky 31, Lucky 63 and higher Lucky bets form a family of bets known as full cover bets with singles
Full cover bet
A full cover bet is any bet which consists of all available multiple bets over a given number of selections.Examples of full cover bets:* Trixie - three selections* Yankee - four selections* Canadian or Super Yankee - five selections...
which have all possible multiples present together with single bets on all selections. An examples of a winning Patent bet has been shown above. The other named bets are calculated in a similar way by looking at all the possible combinations of selections in their multiples and singles.
Should a selection in one of these bets not win, then the remaining winners are treated as being a wholly successful bet on the next 'family member' down. For example, only two winners out of three in a Patent means the bet is settled as a double and two singles; only three winners out of four in a Lucky 15 means it is settled as a Patent; only four winners out of six in a Lucky 63 means it is settled as a Lucky 15. The place part of each-way bets is calculated separately using reduced place odds. Thus, an each-way Lucky 63 on six horses with three winners and a further two placed horses is settled as a win Patent and a place Lucky 31.
Algebraic interpretation
Returns on any bet may be considered to be calculated as 'stake unit' × 'odds multiplier'. The overall 'odds multiplier' is a combined decimal odds value and is the result of all the individual bets that make up a full cover bet, including singles if needed. E.g. if a successful £10 Yankee returned £461.35 then the overall 'odds multiplier' (OM) is 46.135.If a, b, c, d... represent the decimal odds, i.e. (fractional odds + 1), then an OM can be calculated algebraically by multiplying the expressions (a + 1), (b + 1), (c + 1)... etc. together in the required manner and subtracting 1. If required, (decimal odds + 1) may be replaced by (fractional odds + 2).
Examples
3 selections with decimal odds a, b and c.Expanding (a + 1)(b + 1)(c + 1) algebraically gives abc + ab + ac + bc + a + b + c + 1. This is equivalent to the OM for a Patent (treble: abc; doubles: ab, ac and bc; singles: a, b and c) plus 1.
Therefore to calculate the returns for a winning Patent it is just a case of multiplying (a + 1), (b + 1) and (c + 1) together and subtracting 1 to get the OM for the winning bet, i.e. OM = (a + 1)(b + 1)(c + 1) − 1. Now multiply by the unit stake to get the total return on the bet.
E.g. The winning Patent described earlier can be more quickly and simply evaluated by the following:
- Total returns = £2 × [(4/6 + 2) × (2/1 + 2) × (11/4 + 2) − 1] = £99.33
Ignoring any bonuses, a 50 pence each-way Lucky 63 (total stake £63) with 4 winners [2-1, 5-2, 7-2 (all
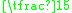odds a place) and 6-4 ( 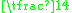odds a place)] and a further placed horse [9-2 ( 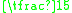odds a place)] can be relatively easily calculated as follows:- Returns (win part) = 0.50 × [(2/1 + 2) × (5/2 + 2) × (7/2 + 2) × (6/4 + 2) − 1] = £172.75
- or more simply as 0.50 × (4 × 4.5 × 5.5 × 3.5 − 1)
- Returns (place part) = 0.50 × [(2/5 + 2) × (5/10 + 2) × (7/10 + 2) × (6/16 + 2) × (9/10 + 2) − 1] = £11.79
- or more simply as 0.50 × (2.4 × 2.5 × 2.7 × 2.375 × 2.9 − 1)
- Total returns = £184.54
For the family of full cover bets that do not include singles an adjustment to the calculation is made to leave just the doubles, trebles and accumulators. Thus, a previously described winning £10 Yankee with winners at 1-3, 5-2, 6-4 and Evens has returns calculated by:
- £10 × [(1/3 + 2) × (5/2 + 2) × (6/4 + 2) × (1/1 + 2) − 1 − [(1/3 + 1) + (5/2 + 1) + (6/4 + 1) + (1/1 + 1)]] = £999.16
In effect, the bet has been calculated as a Lucky 15 minus the singles. Note that the total returns value of £999.16 is a penny higher than the previously calculated value as this quicker method only involves rounding the final answer, and not rounding at each individual step.
In algebraic terms the OM for the Yankee bet is given by:
- OM = (a + 1)(b + 1)(c + 1)(d + 1) − 1 − (a + b + c + d)
In the days before software became available for use by bookmakers and those settling bets in Licensed Betting Offices (LBOs) this method was virtually de rigueur for saving time and avoiding the multiple repetitious calculations necessary in settling bets of the full cover type.
Settling other types of winning bets
Up and down- Returns (£20 single at 7-2 ATC £20 single at 15-8) = £20 × 7/2 + £20 × (15/8 + 1) = £127.50
- Returns (£20 single at 15-8 ATC £20 single at 7-2) = £20 × 15/8 + £20 × (7/2 + 1) = £127.50
- Total returns = £255.00
- Note: This is the same as two £20 single bets at twice the odds; i.e. £20 singles at 7-1 and 15-4 and is the preferred manual way of calculating the bet.
- Returns (£10 single at 5-1 ATC £10 single on 'loser') = £10 × 5/1 = £50
- Note: This calculation of a bet where the stake is not returned is called "receiving the odds to the stake" on the winner; in this case receiving the odds to £10 (on the 5-1 winner).
Round Robin
A Round Robin with 3 winners is calculated as a Trixie plus three Up and Down bets with 2 winners in each.
A Round Robin with 2 winners is calculated as a double plus one Up and Down bet with 2 winners plus two Up and Down bets with 1 winner in each.
A Round Robin with 1 winner is calculated two Up and Down bets with one winner in each.
Flag and Super Flag bets may be calculated in a similar manner as above using the appropriate full cover bet (if sufficient winners) together with the required number of 2 winner- and 1 winner Up and Down bets.
Note: Expert bet settlers before the introduction of bet-settling software would have invariably used an algebraic-type method together with a simple calculator to determine the return on a bet (see below).
Algebraic interpretation
If a, b, c, d... represent the decimal odds, i.e. (fractional odds + 1), then an 'odds multiplier' OM can be calculated algebraically by multiplying the expressions (a + 1), (b + 1), (c + 1)... etc. together in the required manner and adding or subtracting additional components. If required, (decimal odds + 1) may be replaced by (fractional odds + 2).Examples
- OM (2 winners) = (2a − 1) + (2b − 1) = 2(a + b − 1)
- OM (1 winner) = a − 1
- OM (3 winners) = (a + 1) × (b + 1) × (c + 1) − 1 − (a + b + c) + 2 × [(a + b − 1) + (a + c − 1) + (b + c − 1)] = (a + 1)(b + 1)(c + 1) + 3(a + b + c) − 7
- OM (2 winners) = (a + 1) × (b + 1) − 1 − (a + b) + 2 × (a + b − 1) + (a − 1) + (b − 1) = (a + 1)(b + 1) + 2(a + b) − 5
or more simply as OM = ab + 3(a + b) − 4
- OM (1 winner) = 2 × (a − 1) = 2(a − 1)
- OM (4 winners) = (a + 1) × (b + 1) × (c + 1) × (d + 1) − 1 − (a + b + c + d) + 2 × [(a + b − 1) + (a + c − 1) + (a + d − 1) + (b + c − 1) + (b + d − 1) + (c + d − 1)]
= (a + 1)(b + 1)(c + 1)(d + 1) + 5(a + b + c + d) − 13
- OM (3 winners) = (a + 1) × (b + 1) × (c + 1) − 1 − (a + b + c) + 2 × [(a + b − 1) + (a + c − 1) + (b + c − 1)] + (a − 1) + (b − 1) + (c − 1) = (a + 1)(b + 1)(c + 1) + 4(a + b + c) − 10
- OM (2 winners) = (a + 1) × (b + 1) − 1 − (a + b) + 2 × (a + b − 1) + 2 × [(a − 1) + (b − 1)] = (a + 1)(b + 1) + 3(a + b) − 7
or more simply as OM = ab + 4(a + b) − 6
- OM (1 winner) = 3 × (a − 1) = 3(a − 1)
See also
- Glossary of bets offered by UK bookmakersGlossary of bets offered by UK bookmakersThis glossary of bets offered by UK bookmakers is a non-exhaustive list of traditional and popular bets offered by bookmakers in the United Kingdom...
- Statistical association football predictions
Further reading
- "How to make a book", Phil BullPhil BullPhil Bull was a professional gambler, racehorse owner and publisher, who founded Portway Press Ltd, publishers of Timeform racehorse rating guides, one of the most well-known form guides for British horse racing.-Early life:...
, London: Morrison & Gibb Ltd., 1948, 160pp. - "The book on bookmaking", Ferde Rombola, California: Romford Press, 1984, 147pp. 13-digit ISBN 9780935536379 10-digit ISBN 093553637X.
- The Art of Bookmaking, Malcolm Boyle, High Stakes Publishing 2006.
- Secrets of Successful Betting, Michael Adams, Raceform, 2002.
- The Mathematics of Games and Gamblinghttp://www.bjmath.com/bjmath/thorp/tog.htm, Edward W. Packel, Mathematical Association of AmericaMathematical Association of AmericaThe Mathematical Association of America is a professional society that focuses on mathematics accessible at the undergraduate level. Members include university, college, and high school teachers; graduate and undergraduate students; pure and applied mathematicians; computer scientists;...
, 2006. - The Mathematics of Gambling, Edward O. Thorp, L. Stuart, 1984.
- "Maximin Hedges", Jean-Claude Derderian, Mathematics MagazineMathematics MagazineMathematics Magazine is a refereed bimonthly publication of the Mathematical Association of America. Its intended audience is teachers of collegiate mathematics, especially at the junior/senior level, and their students. It is explicitly a journal of mathematics rather than pedagogy...
, volume 51, number 3. (May, 1978), pages 188–192. - "Carnap and de Finetti on Bets and the Probability of Singular Events: The Dutch BookDutch bookIn gambling a Dutch book or lock is a set of odds and bets which guarantees a profit, regardless of the outcome of the gamble. It is associated with probabilities implied by the odds not being coherent....
Argument Reconsidered" Klaus Heilig, The British Journal for the Philosophy of Science, volume 29, number 4. (December, 1978), pages 325–346. - "Tests of the Efficiency of Racetrack Betting Using Bookmaker Odds", Ron Bird, Michael McCrae, Management Science, volume 33, number 12 (December, 1987), pages 152–156.
- "Why is There a Favourite-Longshot Bias in British Racetrack Betting Markets", Leighton Vaughan Williams, David Paton. The Economic Journal, volume 107, number 440 (January, 1997), pages 150–158.
- Optimal Determination of Bookmakers' Betting Odds: Theory and Tests, by John Fingleton and Patrick Waldron, Trinity Economic Paper Series, Technical Paper No. 96/9, Trinity College, University of Dublin, 1999.
- "Odds That Don't Add Up!", Mike Fletcher, Teaching Mathematics and its Applications, 1994, volume 13, number 4, pages 145–147.
- "Information, Prices and Efficiency in a Fixed-Odds Betting Market", Peter F. Pope, David A. Peel, Economica, New Series, volume 56, number 223, (August, 1989), pages 323–341.
- "A Mathematical Perspective on Gambling", Molly Maxwell, MIT Undergraduate Journal of Mathematics, volume 1, (1999), pages 123–132.
- "Probability Guide to Gambling: The Mathematics of dice, slots, roulette, baccarat, blackjack, poker, lottery and sport bets", Catalin Barboianu, Infarom, 2006, 316pp. 10-digit ISBN 9738752035.
External links
- Betting Maths, website dedicated to football betting, examining and explaining statistics, probabilities and portfolio value betting
- online-betting-guide, interactive site explaining basic concepts of several aspects of bookmaking and understanding odds
- bet calculator, choose number of selections and enter odds and stake to calculate win, each-way single and full multiple bets and overround.
- Optimal Price-Setting in Fixed-Odds Betting Markets Under Information Uncertainty by Vasiliki A. Makropoulou of Athens University of Economics and Business and Raphael N. Markellos of Loughborough UniversityLoughborough UniversityLoughborough University is a research based campus university located in the market town of Loughborough, Leicestershire, in the East Midlands of England...
- decimal and fraction odds, explains the difference between decimal and fraction odds when betting.
- bet management, the use of bet staking and weighting plans.