Maupertuis' principle
Encyclopedia
In classical mechanics
, Maupertuis' principle (named after Pierre Louis Maupertuis
) is an integral equation that determines the path followed by a physical system without specifying the time parameterization of that path. It is a special case of the more generally stated principle of least action
. More precisely, it is a formulation of the equations of motion for a physical system not as differential equation
s, but as an integral equation
, using the calculus of variations
.
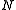generalized coordinates
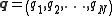between two specified states 
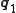and 
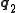is an extremum (i.e., a stationary point
, a minimum, maximum or saddle point) of the abbreviated action
functional
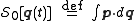
where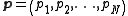
are the conjugate momenta of the generalized coordinates, defined by the equation
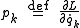
where
is the Lagrangian
function
for the system. In other words, any first-order perturbation of the path results in (at most) second-order changes in
. That the abbreviated action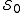 
is not a function
, but a functional
, i.e., something that takes as its input a function
(in this case, the path between the two specified states) and returns a single number, a scalar
.
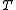is quadratic in the generalized velocities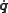 
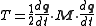
although the mass tensor
may be a complicated function of the generalized coordinates 
. For such systems, a simple relation relates the kinetic energy, the generalized momenta and the generalized velocities
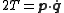
provided that the potential energy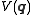
does not involve the generalized velocities. By defining a normalized distance or metric
in the space of generalized coordinates
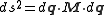
one may immediately recognize the mass tensor as a metric tensor
. The kinetic energy may be written in a massless form
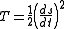
or, equivalently,
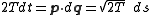
Hence, the abbreviated action can be written
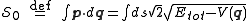
since the kinetic energy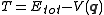
equals the (constant) total energy 
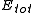minus the potential energy 
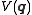. In particular, if the potential energy is a constant, then Jacobi's principle reduces to minimizing the path length 
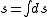in the space of the generalized coordinates, which is equivalent to Hertz's principle of least curvature.
and Maupertuis' principle are occasionally confused and both have been called the principle of least action
. They differ from each other in three important ways:
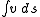, which was to be minimized over all paths connecting two specified points. However, Maupertuis applied the principle only to light, not matter (see the 1744 Maupertuis reference below). He arrived at the principle by considering Snell's law
for the refraction
of light
, which Fermat had explained by Fermat's principle
, that light follows the path of shortest time, not distance. This troubled Maupertuis, since he felt that time and distance should be on an equal footing: "why should light prefer the path of shortest time over that of distance?" Accordingly, Maupertuis asserts with no further justification the principle of least action as equivalent but more fundamental than Fermat's principle
, and uses it to derive Snell's law
. Maupertuis specifically states that light does not follow the same laws as material objects.
A few months later, well before Maupertuis' work appeared in print, Euler independently defined action in its modern abbreviated form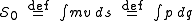
and applied it to the motion of a particle, but not to light (see the 1744 Euler reference below). Euler also recognized that the principle only held when the speed was a function only of position, i.e., when the total energy was conserved. (The mass factor in the action and the requirement for energy conservation were not relevant to Maupertuis, who was concerned only with light.) Euler used this principle to derive the equations of motion of a particle in uniform motion, in a uniform and non-uniform force field, and in a central force field. Euler's approach is entirely consistent with the modern understanding of Maupertuis' principle described above, except that he insisted that the action should always be a minimum, rather than a stationary point.
Two years later, Maupertuis cites Euler's 1744 work as a "beautiful application of my principle to the motion of the planets" and goes on to apply the principle of least action to the lever problem in mechanical equilibrium and to perfectly elastic and perfectly inelastic collisions (see the 1746 publication below). Thus, Maupertuis takes credit for conceiving the principle of least action as a general principle applicable to all physical systems (not merely to light), whereas the historical evidence suggests that Euler was the one to make this intuitive leap. Remarkably, Maupertuis' definitions of the action and protocols for minimizing it in this paper are inconsistent with the modern approach described above. Thus, Maupertuis' published work does not contain a single example in which he used Maupertuis' principle (as presently understood).
In 1751, Maupertuis' priority for the principle of least action was challenged in print (Nova Acta Eruditorum of Leipzig) by an old acquaintance, Johann Samuel Koenig, who quoted a 1707 letter purportedly from Leibniz
that described results similar to those derived by Euler in 1744. However, Maupertuis and others demanded that Koenig produce the original of the letter to authenticate its having been written by Leibniz. Koenig only had a copy and no clue as to the whereabouts of the original. Consequently, the Berlin Academy under Euler's direction declared the letter to be a forgery and that its President Maupertuis could continue to claim priority for having invented the principle. Koenig continued to fight for Leibniz's priority and soon luminaries such as Voltaire
and the King of Prussia, Frederick II
were engaged in the quarrel. However, no progress was made until the turn of the twentieth century, when other independent copies of Leibniz's letter were discovered. The present scholarly consensus seems to be that the quotations from Leibniz are indeed genuine, i.e., that he had invented Maupertuis' principle and applied it to several mechanical problems by 1707 (37 years before Maupertuis and Euler) but did not publish his findings.
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, Maupertuis' principle (named after Pierre Louis Maupertuis
Pierre Louis Maupertuis
Pierre-Louis Moreau de Maupertuis was a French mathematician, philosopher and man of letters. He became the Director of the Académie des Sciences, and the first President of the Berlin Academy of Science, at the invitation of Frederick the Great....
) is an integral equation that determines the path followed by a physical system without specifying the time parameterization of that path. It is a special case of the more generally stated principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
. More precisely, it is a formulation of the equations of motion for a physical system not as differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, but as an integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
, using the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
.
Mathematical formulation
Maupertuis' principle states that the true path of a system described by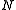 generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
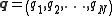between two specified states 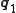and 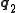is an extremum (i.e., a stationary pointStationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
, a minimum, maximum or saddle point) of the abbreviated action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
functional
Functional
Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
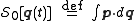
where
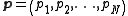are the conjugate momenta of the generalized coordinates, defined by the equation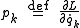where
is the LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
for the system. In other words, any first-order perturbation of the path results in (at most) second-order changes in
. That the abbreviated action 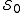is not a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, but a functional
Functional
Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
, i.e., something that takes as its input a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
(in this case, the path between the two specified states) and returns a single number, a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
.
Jacobi's formulation
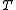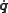
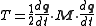
For many systems, the kinetic energy is quadratic in the generalized velocities although the mass tensor
may be a complicated function of the generalized coordinates . For such systems, a simple relation relates the kinetic energy, the generalized momenta and the generalized velocities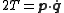provided that the potential energy
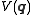does not involve the generalized velocities. By defining a normalized distance or metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
in the space of generalized coordinates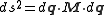one may immediately recognize the mass tensor as a metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. The kinetic energy may be written in a massless form
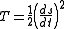
or, equivalently,
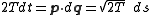
Hence, the abbreviated action can be written
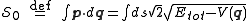
since the kinetic energy
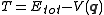equals the (constant) total energy 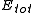minus the potential energy 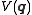. In particular, if the potential energy is a constant, then Jacobi's principle reduces to minimizing the path length 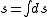in the space of the generalized coordinates, which is equivalent to Hertz's principle of least curvature.Comparison with Hamilton's principle
Hamilton's principleHamilton's principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
and Maupertuis' principle are occasionally confused and both have been called the principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
. They differ from each other in three important ways:
- their definition of the actionAction (physics)In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
...
-
-
- Hamilton's principle uses
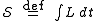, the integral of the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
over timeTimeTime is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, varied between two fixed end times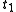
, 
and endpoints 
, 
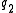. By contrast, Maupertuis' principle uses the abbreviated action integral over the generalized coordinatesGeneralized coordinatesIn the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
, varied along all constant energy paths ending at
and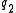 
.
- Hamilton's principle uses
-
- the solution that they determine...
-
-
- Hamilton's principle determines the trajectory
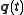as a function of time, whereas Maupertuis' principle determines only the shape of the trajectory in the generalized coordinates. For example, Maupertuis' principle determines the shape of the ellipse on which a particle moves under the influence of an inverse-square central force such as gravityGravitationGravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
, but does not describe per se how the particle moves along that trajectory. (However, this time parameterization may be determined from the trajectory itself in subsequent calculations using the conservation of energy.) By contrast, Hamilton's principle directly specifies the motion along the ellipse as a function of time.
- Hamilton's principle determines the trajectory
-
- ...and the constraints on the variation.
-
-
- Maupertuis' principle requires that the two endpoint states
and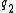 
be given and that energy be conserved along every trajectory. By contrast, Hamilton's principle does not require the conservation of energy, but does require that the endpoint times 
and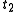 
be specified as well as the endpoint states 
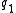and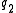 
.
- Maupertuis' principle requires that the two endpoint states
-
History
Maupertuis was the first to publish a principle of least action, where he defined action as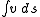, which was to be minimized over all paths connecting two specified points. However, Maupertuis applied the principle only to light, not matter (see the 1744 Maupertuis reference below). He arrived at the principle by considering Snell's lawSnell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
for the refraction
Refraction
Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
of light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
, which Fermat had explained by Fermat's principle
Fermat's principle
In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light...
, that light follows the path of shortest time, not distance. This troubled Maupertuis, since he felt that time and distance should be on an equal footing: "why should light prefer the path of shortest time over that of distance?" Accordingly, Maupertuis asserts with no further justification the principle of least action as equivalent but more fundamental than Fermat's principle
Fermat's principle
In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light...
, and uses it to derive Snell's law
Snell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
. Maupertuis specifically states that light does not follow the same laws as material objects.
A few months later, well before Maupertuis' work appeared in print, Euler independently defined action in its modern abbreviated form
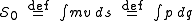and applied it to the motion of a particle, but not to light (see the 1744 Euler reference below). Euler also recognized that the principle only held when the speed was a function only of position, i.e., when the total energy was conserved. (The mass factor in the action and the requirement for energy conservation were not relevant to Maupertuis, who was concerned only with light.) Euler used this principle to derive the equations of motion of a particle in uniform motion, in a uniform and non-uniform force field, and in a central force field. Euler's approach is entirely consistent with the modern understanding of Maupertuis' principle described above, except that he insisted that the action should always be a minimum, rather than a stationary point.Two years later, Maupertuis cites Euler's 1744 work as a "beautiful application of my principle to the motion of the planets" and goes on to apply the principle of least action to the lever problem in mechanical equilibrium and to perfectly elastic and perfectly inelastic collisions (see the 1746 publication below). Thus, Maupertuis takes credit for conceiving the principle of least action as a general principle applicable to all physical systems (not merely to light), whereas the historical evidence suggests that Euler was the one to make this intuitive leap. Remarkably, Maupertuis' definitions of the action and protocols for minimizing it in this paper are inconsistent with the modern approach described above. Thus, Maupertuis' published work does not contain a single example in which he used Maupertuis' principle (as presently understood).
In 1751, Maupertuis' priority for the principle of least action was challenged in print (Nova Acta Eruditorum of Leipzig) by an old acquaintance, Johann Samuel Koenig, who quoted a 1707 letter purportedly from Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
that described results similar to those derived by Euler in 1744. However, Maupertuis and others demanded that Koenig produce the original of the letter to authenticate its having been written by Leibniz. Koenig only had a copy and no clue as to the whereabouts of the original. Consequently, the Berlin Academy under Euler's direction declared the letter to be a forgery and that its President Maupertuis could continue to claim priority for having invented the principle. Koenig continued to fight for Leibniz's priority and soon luminaries such as Voltaire
Voltaire
François-Marie Arouet , better known by the pen name Voltaire , was a French Enlightenment writer, historian and philosopher famous for his wit and for his advocacy of civil liberties, including freedom of religion, free trade and separation of church and state...
and the King of Prussia, Frederick II
Frederick II of Prussia
Frederick II was a King in Prussia and a King of Prussia from the Hohenzollern dynasty. In his role as a prince-elector of the Holy Roman Empire, he was also Elector of Brandenburg. He was in personal union the sovereign prince of the Principality of Neuchâtel...
were engaged in the quarrel. However, no progress was made until the turn of the twentieth century, when other independent copies of Leibniz's letter were discovered. The present scholarly consensus seems to be that the quotations from Leibniz are indeed genuine, i.e., that he had invented Maupertuis' principle and applied it to several mechanical problems by 1707 (37 years before Maupertuis and Euler) but did not publish his findings.
See also
- Analytical mechanicsAnalytical mechanicsAnalytical mechanics is a term used for a refined, mathematical form of classical mechanics, constructed from the 18th century onwards as a formulation of the subject as founded by Isaac Newton. Often the term vectorial mechanics is applied to the form based on Newton's work, to contrast it with...
- Hamilton's principleHamilton's principleIn physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
- Gauss' principle of least constraint (also describes Hertz's principle of least curvature)
- Hamilton–Jacobi equationHamilton–Jacobi equationIn mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...