Maxwell-Stefan diffusion
Encyclopedia
The Maxwell–Stefan diffusion (or Stefan–Maxwell diffusion) is a model
for describing diffusion
in multicomponent systems. The equations that describe these transport processes have been developed independently and in parallel by James Clerk Maxwell
for dilute gases and Josef Stefan for fluids. The Maxwell–Stefan equation is :
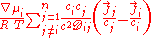
The equation assumes steady state
, that is the absence of velocity gradients.
The basic assumption of the theory is that a deviation from equilibrium between the molecular friction and thermodynamic interactions leads to the diffusion flux. The molecular friction between two components is proportional to their difference in speed and their mole fractions. In the simplest case, the gradient
of chemical potential is the driving force of diffusion. For complex systems, such as electrolytic solutions, and other drivers, such as a pressure gradient, the equation must be expanded to include additional terms for interactions.
A major disadvantage of the Maxwell–Stefan theory is that the diffusion coefficients, with the exception of the diffusion of dilute gases, do not correspond to the Fick's diffusion coefficients and are therefore not tabulated. Only the diffusion coefficients for the binary and ternary case can be determined with reasonable effort. In a multicomponent system, a set of approximate formulas exist to predict the Maxwell–Stefan-diffusion coefficient.
The Maxwell–Stefan theory is more comprehensive than the "classical" Fick's diffusion theory, as the former does not exclude the possibility of negative diffusion coefficients. It is possible to derive Fick's theory from the Maxwell–Stefan theory.
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
for describing diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
in multicomponent systems. The equations that describe these transport processes have been developed independently and in parallel by James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
for dilute gases and Josef Stefan for fluids. The Maxwell–Stefan equation is :
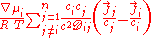
- ∇: vector differential operatorDelIn vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
- χ: Mole fraction
- μ: Chemical potentialChemical potentialChemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
- a: ActivityActivity (chemistry)In chemical thermodynamics, activity is a measure of the “effective concentration” of a species in a mixture, meaning that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution.By convention, activity...
- i, j: Indexes for component i and j
- n: Number of components
-
: Maxwell–Stefan-diffusion coefficient -
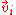: Diffusion velocity of component i -
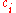: Molar concentration of component i - c: Total molar concentration
-
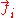: FluxFluxIn the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
of component i
The equation assumes steady state
Steady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
, that is the absence of velocity gradients.
The basic assumption of the theory is that a deviation from equilibrium between the molecular friction and thermodynamic interactions leads to the diffusion flux. The molecular friction between two components is proportional to their difference in speed and their mole fractions. In the simplest case, the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of chemical potential is the driving force of diffusion. For complex systems, such as electrolytic solutions, and other drivers, such as a pressure gradient, the equation must be expanded to include additional terms for interactions.
A major disadvantage of the Maxwell–Stefan theory is that the diffusion coefficients, with the exception of the diffusion of dilute gases, do not correspond to the Fick's diffusion coefficients and are therefore not tabulated. Only the diffusion coefficients for the binary and ternary case can be determined with reasonable effort. In a multicomponent system, a set of approximate formulas exist to predict the Maxwell–Stefan-diffusion coefficient.
The Maxwell–Stefan theory is more comprehensive than the "classical" Fick's diffusion theory, as the former does not exclude the possibility of negative diffusion coefficients. It is possible to derive Fick's theory from the Maxwell–Stefan theory.