
Mean-preserving spread
Encyclopedia
In probability and statistics
, a mean-preserving spread (MPS) is a change from one probability distribution
A to another probability distribution B, where B is formed by spreading out one or more portions of A's probability density function
while leaving the mean (the expected value
) unchanged. As such, the concept of mean-preserving spreads provides a stochastic ordering
of equal-mean gambles (probability distributions) according to their degree of risk
; this ordering is partial, meaning that of two equal-mean gambles, it is not necessarily true that either is a mean-preserving spread of the other. Definitionally, if B is a mean-preserving spread of A then A is said to be a mean-preserving contraction of B.
Ranking gambles by mean-preserving spreads is a special case of ranking gambles by second-order stochastic dominance
– namely, the special case of equal means: If B is a mean-preserving spread of A, then A is second-order stochastically dominant over B; and the converse holds if A and B have equal means.
If B is a mean-preserving spread of A, then B has a higher variance than A; but the converse is not in general true, because the variance is a complete ordering while ordering by mean-preserving spreads is only partial.
 on each outcome
on each outcome  , with
, with 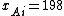 for
for 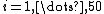 and
and 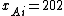 for
for 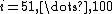 ; and let B have equal probabilities
; and let B have equal probabilities 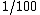 on each outcome
on each outcome 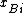 , with
, with 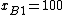 ,
, 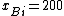 for
for 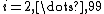 , and
, and 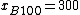 . Here B has been constructed from A by moving one chunk of 1% probability from 198 to 100 and moving 49 probability chunks from 198 to 200, and then moving one probability chunk from 202 to 300 and moving 49 probability chunks from 202 to 200. This sequence of two mean-preserving spreads is itself a mean-preserving spread, despite the fact that 98% of the probability mass has moved to the mean (200).
. Here B has been constructed from A by moving one chunk of 1% probability from 198 to 100 and moving 49 probability chunks from 198 to 200, and then moving one probability chunk from 202 to 300 and moving 49 probability chunks from 202 to 200. This sequence of two mean-preserving spreads is itself a mean-preserving spread, despite the fact that 98% of the probability mass has moved to the mean (200).
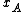 and
and 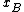 be the random variables associated with gambles A and B. Then B is a mean-preserving spread of A if and only if
be the random variables associated with gambles A and B. Then B is a mean-preserving spread of A if and only if 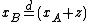 for some random variable
for some random variable  having
having 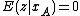 for all values of
for all values of 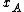 . Here
. Here 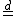 means "is equal in distribution to" (that is, "has the same distribution as").
means "is equal in distribution to" (that is, "has the same distribution as").
Mean-preserving spreads can also be defined in terms of the cumulative distribution function
s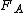 and
and 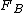 of A and B. If A and B have equal means, B is a mean-preserving spread of A if and only if the area under
of A and B. If A and B have equal means, B is a mean-preserving spread of A if and only if the area under 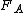 from minus infinity to
from minus infinity to  is less than or equal to that under
is less than or equal to that under 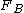 from minus infinity to
from minus infinity to  for all real numbers
for all real numbers  , with strict inequality at some
, with strict inequality at some  .
.
Both of these mathematical definitions replicate those of second-order stochastic dominance for the case of equal means.
maximizers having concave utility. The converse also holds: if A and B have equal means and A is preferred by all expected utility maximizers having concave utility, then B is a mean-preserving spread of A.
Probability and statistics
See the separate articles on probability or the article on statistics. Statistical analysis often uses probability distributions, and the two topics are often studied together. However, probability theory contains much that is of mostly mathematical interest and not directly relevant to statistics...
, a mean-preserving spread (MPS) is a change from one probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
A to another probability distribution B, where B is formed by spreading out one or more portions of A's probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
while leaving the mean (the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
) unchanged. As such, the concept of mean-preserving spreads provides a stochastic ordering
Stochastic ordering
In probability theory and statistics, a stochastic order quantifies the concept of one random variable being "bigger" than another. These are usually partial orders, so that one random variable A may be neither stochastically greater than, less than nor equal to another random variable B...
of equal-mean gambles (probability distributions) according to their degree of risk
Risk
Risk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
; this ordering is partial, meaning that of two equal-mean gambles, it is not necessarily true that either is a mean-preserving spread of the other. Definitionally, if B is a mean-preserving spread of A then A is said to be a mean-preserving contraction of B.
Ranking gambles by mean-preserving spreads is a special case of ranking gambles by second-order stochastic dominance
Stochastic dominance
Stochastic dominance is a form of stochastic ordering. The term is used in decision theory and decision analysis to refer to situations where one gamble can be ranked as superior to another gamble. It is based on preferences regarding outcomes...
– namely, the special case of equal means: If B is a mean-preserving spread of A, then A is second-order stochastically dominant over B; and the converse holds if A and B have equal means.
If B is a mean-preserving spread of A, then B has a higher variance than A; but the converse is not in general true, because the variance is a complete ordering while ordering by mean-preserving spreads is only partial.
Example
This example from shows that to have a mean-preserving spread does not require that all or most of the probability mass move away from the mean. Let A have equal probabilities on each outcome
on each outcome  , with
, with 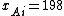 for
for 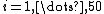 and
and 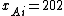 for
for 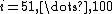 ; and let B have equal probabilities
; and let B have equal probabilities 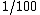 on each outcome
on each outcome 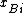 , with
, with 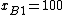 ,
, 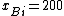 for
for 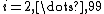 , and
, and 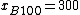 . Here B has been constructed from A by moving one chunk of 1% probability from 198 to 100 and moving 49 probability chunks from 198 to 200, and then moving one probability chunk from 202 to 300 and moving 49 probability chunks from 202 to 200. This sequence of two mean-preserving spreads is itself a mean-preserving spread, despite the fact that 98% of the probability mass has moved to the mean (200).
. Here B has been constructed from A by moving one chunk of 1% probability from 198 to 100 and moving 49 probability chunks from 198 to 200, and then moving one probability chunk from 202 to 300 and moving 49 probability chunks from 202 to 200. This sequence of two mean-preserving spreads is itself a mean-preserving spread, despite the fact that 98% of the probability mass has moved to the mean (200).Mathematical definitions
Let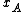 and
and 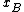 be the random variables associated with gambles A and B. Then B is a mean-preserving spread of A if and only if
be the random variables associated with gambles A and B. Then B is a mean-preserving spread of A if and only if 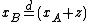 for some random variable
for some random variable  having
having 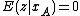 for all values of
for all values of 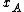 . Here
. Here 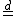 means "is equal in distribution to" (that is, "has the same distribution as").
means "is equal in distribution to" (that is, "has the same distribution as").Mean-preserving spreads can also be defined in terms of the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s
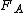 and
and 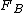 of A and B. If A and B have equal means, B is a mean-preserving spread of A if and only if the area under
of A and B. If A and B have equal means, B is a mean-preserving spread of A if and only if the area under 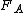 from minus infinity to
from minus infinity to  is less than or equal to that under
is less than or equal to that under 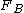 from minus infinity to
from minus infinity to  for all real numbers
for all real numbers  , with strict inequality at some
, with strict inequality at some  .
.Both of these mathematical definitions replicate those of second-order stochastic dominance for the case of equal means.
Relation to expected utility theory
If B is a mean-preserving spread of A then A will be preferred by all expected utilityExpected utility hypothesis
In economics, game theory, and decision theory the expected utility hypothesis is a theory of utility in which "betting preferences" of people with regard to uncertain outcomes are represented by a function of the payouts , the probabilities of occurrence, risk aversion, and the different utility...
maximizers having concave utility. The converse also holds: if A and B have equal means and A is preferred by all expected utility maximizers having concave utility, then B is a mean-preserving spread of A.

