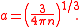Mean inter-particle distance
Encyclopedia
Mean inter-particle distance (or mean inter-particle separation) is the mean distance between microscopic particles (usually atoms or molecules) in a macroscopic body.
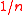 , i.e.,
, i.e.,
where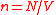 is the particle density
is the particle density
. However, barring a few simple cases such as the ideal gas
model, precise calculations of the proportionality factor are impossible analytically. Therefore, approximate expressions are often used. One such an estimation is the Wigner-Seitz radius
which corresponds to the radius of a sphere having per-particle volume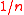 . Another popular definition is
. Another popular definition is
corresponding to the length of the edge of the cube with the per-particle volume . Evidently, the two definitions differ by a factor of
. Evidently, the two definitions differ by a factor of  , thus one has to exercise care if an article fails to define the parameter exactly. On the other hand, it is often used in qualitative statements where such a numeric factor is either irrelevant or plays an insignificant role, e.g.,
, thus one has to exercise care if an article fails to define the parameter exactly. On the other hand, it is often used in qualitative statements where such a numeric factor is either irrelevant or plays an insignificant role, e.g.,
of distance to the nearest neighbor (NN) particle. (The problem was first considered by Paul Hertz; for a modern derivation see, e.g.,.) Let us assume particles inside a sphere having volume
particles inside a sphere having volume 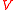 , so that
, so that 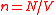 . Note that since the particles in the ideal gas are non-interacting, the probability to find a particle at a certain distance from another particle is the same as probability to find a particle at the same distance from any other point; we shall use the center of the sphere.
. Note that since the particles in the ideal gas are non-interacting, the probability to find a particle at a certain distance from another particle is the same as probability to find a particle at the same distance from any other point; we shall use the center of the sphere.
An NN particle at distance means exactly one of the
means exactly one of the  particles resides at that distance while the rest
particles resides at that distance while the rest
 particles are at larger distances, i.e., they are somewhere outside the sphere with radius
particles are at larger distances, i.e., they are somewhere outside the sphere with radius  .
.
The probability to find a particle at the distance from the origin between and
and  is
is
 , while the probability to find a particle outside that sphere is
, while the probability to find a particle outside that sphere is  . The sought-for expression is then
. The sought-for expression is then
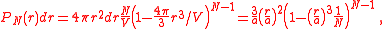
where we substituted
Finally, taking the limit and using
limit and using 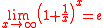 , we obtain
, we obtain
|
|}
One can immediately check that
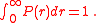
The distribution peaks at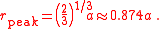

or, using the substitution,
substitution,
where is the gamma function
is the gamma function
. Thus,
|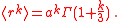
|}
In particular,
|
|}
Ambiguity
From the very general considerations, the mean inter-particle distance is proportional to the size of the per-particle volume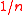 , i.e.,
, i.e.,
where
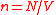 is the particle density
is the particle densityParticle density
The particle density or true density of a particulate solid or powder, is the density of the particles that make up the powder, in contrast to the bulk density, which measures the average density of a large volume of the powder in a specific medium .The particle density is a relatively well-defined...
. However, barring a few simple cases such as the ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
model, precise calculations of the proportionality factor are impossible analytically. Therefore, approximate expressions are often used. One such an estimation is the Wigner-Seitz radius
Wigner-Seitz radius
The Wigner–Seitz radius r_s, named after Eugene Wigner and Frederick Seitz, is a parameter used frequently in condensed matter physics to describe the density of a system...
which corresponds to the radius of a sphere having per-particle volume
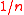 . Another popular definition is
. Another popular definition is
-
 ,
,
corresponding to the length of the edge of the cube with the per-particle volume
 . Evidently, the two definitions differ by a factor of
. Evidently, the two definitions differ by a factor of  , thus one has to exercise care if an article fails to define the parameter exactly. On the other hand, it is often used in qualitative statements where such a numeric factor is either irrelevant or plays an insignificant role, e.g.,
, thus one has to exercise care if an article fails to define the parameter exactly. On the other hand, it is often used in qualitative statements where such a numeric factor is either irrelevant or plays an insignificant role, e.g.,- "a potential energy ... is proportional to some power n of the inter-particle distance r" (Virial theorem)
- "the inter-particle distance is much larger than the thermal de Broglie wavelength" (Kinetic theoryKinetic theoryThe kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container...
)
Nearest neighbor distribution
We want to calculate probability distribution functionProbability distribution function
Depending upon which text is consulted, a probability distribution function is any of:* a probability distribution function,* a cumulative distribution function,* a probability mass function, or* a probability density function....
of distance to the nearest neighbor (NN) particle. (The problem was first considered by Paul Hertz; for a modern derivation see, e.g.,.) Let us assume
 particles inside a sphere having volume
particles inside a sphere having volume 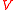 , so that
, so that 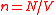 . Note that since the particles in the ideal gas are non-interacting, the probability to find a particle at a certain distance from another particle is the same as probability to find a particle at the same distance from any other point; we shall use the center of the sphere.
. Note that since the particles in the ideal gas are non-interacting, the probability to find a particle at a certain distance from another particle is the same as probability to find a particle at the same distance from any other point; we shall use the center of the sphere.An NN particle at distance
 means exactly one of the
means exactly one of the  particles resides at that distance while the rest
particles resides at that distance while the rest particles are at larger distances, i.e., they are somewhere outside the sphere with radius
particles are at larger distances, i.e., they are somewhere outside the sphere with radius  .
.The probability to find a particle at the distance from the origin between
 and
and  is
is , while the probability to find a particle outside that sphere is
, while the probability to find a particle outside that sphere is  . The sought-for expression is then
. The sought-for expression is then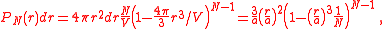
where we substituted
Finally, taking the
 limit and using
limit and using 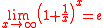 , we obtain
, we obtain-
- {|cellpadding="2" style="border:2px solid #ccccff"
|

|}
One can immediately check that
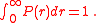
The distribution peaks at
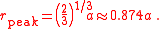
Mean distance and higher NN distribution moments

or, using the
 substitution,
substitution,
where
 is the gamma function
is the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. Thus,
-
- {|cellpadding="2" style="border:2px solid #ccccff"
|
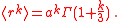
|}
In particular,
-
- {|cellpadding="2" style="border:2px solid #ccccff"
|

|}