Mean width
Encyclopedia
In geometry, the mean width is a measure of dimension length of the "size" a body; see Hadwiger's theorem
for more about the available measures of bodies. In
dimensions, one has to consider 
-dimensional hyperplanes perpendicular to a given direction 
in 
, where 
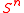is the n-sphere (the surface of a 
-dimensional sphere).
The "width" of a body in a given direction
is the distance between the closest pair of such planes, such that the body is entirely in between the two hyper planes (the planes only intersect
with the boundary of the body). The mean width is the average of this "width" over all
in 
.
More formally, define a compact body B as being equivalent to set of points in its interior plus the points on the boundary (here, points denote elements of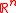
). The support function of body B is defined as
where
is a direction and 
denotes the usual inner product on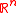 
. The mean width is then
where
is the 
-dimensional volume of 
.
Note, that the mean width can be defined for any body (that is compact), but it is most
useful for convex bodies (that is bodies, whose corresponding set is a convex set
).
, H, over the whole surface of K. In fact,
where
is the boundary of the convex body 
and 
a surface integral element,
is the mean curvature
at the corresponding position
on
. Similar relations can be given between the other measures
and the generalizations of the mean curvature, also for other dimensions
.
As the integral over the mean curvature is typically much easier to calculate
than the mean width, this is a very useful result.
The application of the mean width as one of the measures featuring in Hadwiger's theorem
is discussed in Beifang Chen in "A simplified elementary proof of Hadwiger's volume theorem." Geom. Dedicata 105 (2004), 107—120.
Hadwiger's theorem
In integral geometry , Hadwiger's theorem characterises the valuations on convex bodies in Rn. It was proved by Hugo Hadwiger.-Valuations:...
for more about the available measures of bodies. In
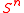dimensions, one has to consider -dimensional hyperplanes perpendicular to a given direction in , where is the n-sphere (the surface of a -dimensional sphere).The "width" of a body in a given direction
is the distance between the closest pair of such planes, such that the body is entirely in between the two hyper planes (the planes only intersectwith the boundary of the body). The mean width is the average of this "width" over all
in .More formally, define a compact body B as being equivalent to set of points in its interior plus the points on the boundary (here, points denote elements of
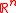). The support function of body B is defined as
where
is a direction and denotes the usual inner product on 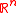. The mean width is then
where
is the -dimensional volume of .Note, that the mean width can be defined for any body (that is compact), but it is most
useful for convex bodies (that is bodies, whose corresponding set is a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
).
The relation between mean width and mean curvature
For convex bodies K in three dimensions, the mean width of K is related to the average of the mean curvatureMean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
, H, over the whole surface of K. In fact,
where
is the boundary of the convex body and a surface integral element,
is the mean curvatureMean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
at the corresponding position
on
. Similar relations can be given between the other measuresand the generalizations of the mean curvature, also for other dimensions
.
As the integral over the mean curvature is typically much easier to calculate
than the mean width, this is a very useful result.
Reference material
The mean width is usually mentioned in any good reference on convex geometry, for instance, Selected topics in convex geometry by Maria Moszyńska (Birkhäuser, Boston 2006). The relation between the mean width and the mean curvature is also derived in that reference.The application of the mean width as one of the measures featuring in Hadwiger's theorem
Hadwiger's theorem
In integral geometry , Hadwiger's theorem characterises the valuations on convex bodies in Rn. It was proved by Hugo Hadwiger.-Valuations:...
is discussed in Beifang Chen in "A simplified elementary proof of Hadwiger's volume theorem." Geom. Dedicata 105 (2004), 107—120.