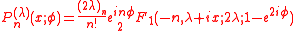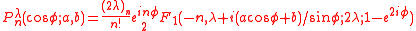Meixner–Pollaczek polynomials
Encyclopedia
In mathematics, the Meixner–Pollaczek polynomials are a family of orthogonal polynomials
P(x,φ) introduced by , which up to elementary changes of variables are the same as the Pollaczek polynomials P(x,a,b) rediscovered by in the case λ=1/2, and later generalized by him.
They are defined by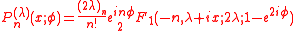
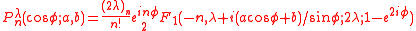
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
P(x,φ) introduced by , which up to elementary changes of variables are the same as the Pollaczek polynomials P(x,a,b) rediscovered by in the case λ=1/2, and later generalized by him.
They are defined by