Mergelyan's theorem
Encyclopedia
Mergelyan's theorem is a famous result from complex analysis
, a branch of mathematics
, named after the Armenian mathematician
Sergei Nikitovich Mergelyan
(May 19, 1928 - August 20, 2008) and was put forward by him in 1951. It states the following:
Let K be a compact subset of the complex plane
C such that C\K is connected. Then, every continuous function
f : K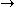
C, such that the restriction f|int(K) is holomorphic
, can be approximated uniformly on K with polynomial
s. Here, int(K) denotes the interior
of K.
Mergelyan's theorem is the ultimate development and generalization of the Weierstrass approximation theorem and Runge's theorem
. It gives the complete solution of the classical problem of approximation by polynomials.
In the case that C\K is not connected, in the initial approximation problem the polynomials have to be replaced by rational functions. An important step of the solution of this further rational approximation problem was also suggested by Mergelyan in 1952. Further deep results on rational approximation are due to, in particular, A.G. Vitushkin.
Weierstrass and Runge's theorems were put forward in 1885, while Mergelyan's theorem dates from 1951. This rather large time difference is not surprising, as the proof of Mergelyan's theorem is based on a new powerful method created by Mergelyan. After Weierstrass and Runge, many mathematicians (in particular Walsh, Keldysh
, and Lavrentyev
) had been working on the same problem.
The method of the proof suggested by Mergelyan is constructive, and remains the only known constructive proof of the result.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, named after the Armenian mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Sergei Nikitovich Mergelyan
Sergey Mergelyan
Sergey Nikitovich Mergelyan was an soviet scientist of Armenian origin, an outstanding mathematician, who is the author of major contributions in Approximation Theory. The modern Complex Approximation Theory is based on Mergelyan's classical work....
(May 19, 1928 - August 20, 2008) and was put forward by him in 1951. It states the following:
Let K be a compact subset of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
C such that C\K is connected. Then, every continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
f : K
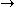C, such that the restriction f|int(K) is holomorphicHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
, can be approximated uniformly on K with polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s. Here, int(K) denotes the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of K.
Mergelyan's theorem is the ultimate development and generalization of the Weierstrass approximation theorem and Runge's theorem
Runge's theorem
In complex analysis, Runge's theorem, also known as Runge's approximation theorem, named after the German Mathematician Carl Runge, and put forward by him in the year 1885, states the following: If K is a compact subset of C , A is a set containing at least one complex number from every bounded...
. It gives the complete solution of the classical problem of approximation by polynomials.
In the case that C\K is not connected, in the initial approximation problem the polynomials have to be replaced by rational functions. An important step of the solution of this further rational approximation problem was also suggested by Mergelyan in 1952. Further deep results on rational approximation are due to, in particular, A.G. Vitushkin.
Weierstrass and Runge's theorems were put forward in 1885, while Mergelyan's theorem dates from 1951. This rather large time difference is not surprising, as the proof of Mergelyan's theorem is based on a new powerful method created by Mergelyan. After Weierstrass and Runge, many mathematicians (in particular Walsh, Keldysh
Keldysh
Keldysh can refer to one of the following.*Leonid Keldysh , a Russian physicist, former director of the Lebedev Physical Institute , now physics faculty at Texas A&M University**Keldysh formalism for studying the Spin Hall effect...
, and Lavrentyev
Mikhail Lavrentyev
Mikhail Alekseevich Lavrentyev or Lavrentiev was an outstanding Soviet mathematician and hydrodynamicist.-Biography:...
) had been working on the same problem.
The method of the proof suggested by Mergelyan is constructive, and remains the only known constructive proof of the result.