
Mertens' theorems
Encyclopedia
In number theory
, Mertens' theorems are three 1874 results related to the density of prime number
s proved by Franz Mertens
(JRAM 78 (1874), 46–62). It may also refer to his theorem in analysis
.
In the following, let mean all primes not exceeding n.
mean all primes not exceeding n.
Mertens' 1st theorem:
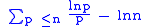
does not exceed 2 in absolute value for every .
.
Mertens' 2nd theorem:

where M is the Meissel–Mertens constant. More precisely, Mertens proves (loc. cit.) that the expression under the limit does not in absolute value exceed
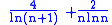
for every .
.
Mertens' 3rd theorem:
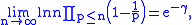
where γ is the Euler–Mascheroni constant
.
In a paper on the growth rate of the sum-of-divisors function published in 1983, Guy Robin proved that in Mertens' 2nd theorem the difference
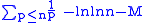
changes sign infinitely often, and that in Mertens' 3rd theorem the difference
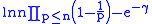
changes sign infinitely often. Robin's results are analogous to Littlewood
's famous theorem that the difference π(x) − li(x) changes sign infinitely often. No analog of the Skewes number (an upper bound on the first natural number
x for which π(x) > li(x)) is known in the case of Mertens' 2nd and 3rd theorems.
In summability theory, Mertens' theorem states that if a real or complex infinite series
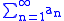
converges to A and another
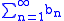
converges absolutely
to B then their Cauchy product converges to AB.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Mertens' theorems are three 1874 results related to the density of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s proved by Franz Mertens
Franz Mertens
Franz Mertens was a German mathematician. He was born in Środa in the Grand Duchy of Poznań, Kingdom of Prussia and died in Vienna, Austria....
(JRAM 78 (1874), 46–62). It may also refer to his theorem in analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
.
In the following, let
 mean all primes not exceeding n.
mean all primes not exceeding n.Mertens' 1st theorem:
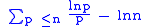
does not exceed 2 in absolute value for every
 .
.Mertens' 2nd theorem:

where M is the Meissel–Mertens constant. More precisely, Mertens proves (loc. cit.) that the expression under the limit does not in absolute value exceed
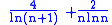
for every
 .
.Mertens' 3rd theorem:
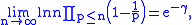
where γ is the Euler–Mascheroni constant
Euler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
.
In a paper on the growth rate of the sum-of-divisors function published in 1983, Guy Robin proved that in Mertens' 2nd theorem the difference
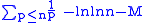
changes sign infinitely often, and that in Mertens' 3rd theorem the difference
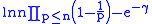
changes sign infinitely often. Robin's results are analogous to Littlewood
John Edensor Littlewood
John Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
's famous theorem that the difference π(x) − li(x) changes sign infinitely often. No analog of the Skewes number (an upper bound on the first natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
x for which π(x) > li(x)) is known in the case of Mertens' 2nd and 3rd theorems.
In summability theory, Mertens' theorem states that if a real or complex infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
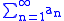
converges to A and another
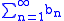
converges absolutely
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
to B then their Cauchy product converges to AB.
Further reading
- Yaglom and Yaglom Challenging mathematical problems with elementary solutions Vol 2, problems 171, 173, 174

