Milliken's tree theorem
Encyclopedia
In mathematics
, Milliken's tree theorem in combinatorics
is a partition theorem generalizing Ramsey's theorem
to infinite trees
, objects with more structure than sets.
Let T be a finitely splitting rooted tree of height ω, n a positive integer, and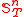
the collection of all strongly embedded subtrees of T of height n. In one of its simple forms, Milliken's tree theorem states that if 
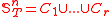then for some strongly embedded infinite subtree R of T, 
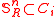for some i ≤ r.
This immediately implies Ramsey's theorem
; take the tree T to be a linear ordering on ω vertices.
Define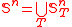
where T ranges over finitely splitting rooted trees of height ω. Milliken's tree theorem says that not only is 
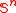partition regular for each n < ω, but that the homogeneous subtree R guaranteed by the theorem is strongly embedded in T.
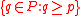, and 
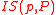to be the set of immediate successors of p in P. Suppose S is an α-tree and T is a β-tree, with 0 ≤ α ≤ β ≤ ω. S is strongly embedded in T if:
Intuitively, for S to be strongly embedded in T,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Milliken's tree theorem in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
is a partition theorem generalizing Ramsey's theorem
Ramsey's theorem
In combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
to infinite trees
Tree (set theory)
In set theory, a tree is a partially ordered set In set theory, a tree is a partially ordered set (poset) In set theory, a tree is a partially ordered set (poset) (T, In set theory, a tree is a partially ordered set (poset) (T, ...
, objects with more structure than sets.
Let T be a finitely splitting rooted tree of height ω, n a positive integer, and
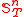the collection of all strongly embedded subtrees of T of height n. In one of its simple forms, Milliken's tree theorem states that if 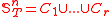then for some strongly embedded infinite subtree R of T, 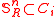for some i ≤ r.This immediately implies Ramsey's theorem
Ramsey's theorem
In combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
; take the tree T to be a linear ordering on ω vertices.
Define
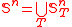where T ranges over finitely splitting rooted trees of height ω. Milliken's tree theorem says that not only is 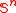partition regular for each n < ω, but that the homogeneous subtree R guaranteed by the theorem is strongly embedded in T.Strong embedding
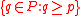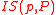Call T an α-tree if each branch of T has cardinality α. Thus each α-tree has height α, but a tree with height α need not be an α-tree. Define Succ(p, P)=, and to be the set of immediate successors of p in P. Suppose S is an α-tree and T is a β-tree, with 0 ≤ α ≤ β ≤ ω. S is strongly embedded in T if:-
, and the partial order on S is induced from T, - if
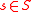is nonmaximal in S and 
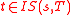, then 
, - there exists a strictly increasing function from
to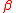 
, such that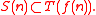 
Intuitively, for S to be strongly embedded in T,
- S must be a subset of T with the induced partial order
- S must preserve the branching structure of T; i.e., if a nonmaximal node in S has n immediate successors in T, then it has n immediate successors in S
- S preserves the level structure of T; all nodes on a common level of S must be on a common level in T.